An algebra of orders

Did you know that we can add and multiply orders? There is a whole algebra of orders, with ℕ+1 and ℤ+ℤ, as well as ℕ+ℤ·ℤ and ℤ·ℚ, a truly fascinating order, discrete but with a dense suborder.

Did you know that you can add and multiply orders? For any two order structures A and B, we can form the ordered sum A + B and ordered product A · B, and other natural operations, such as the disjoint sum A ⊔ B and the cartesian product A × B, which make altogether a rich arithmetic of orders. We combine orders with these operations to make new orders, often with interesting properties. Let us explore the resulting algebra of orders.

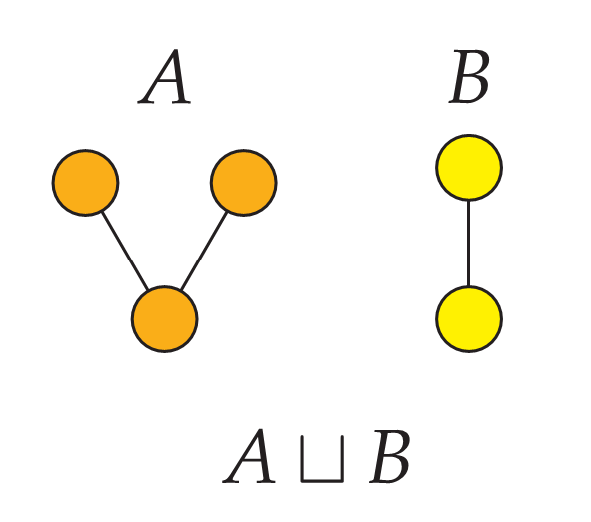
One of the most basic operations that we can use to combine two orders is the disjoint sum operation A ⊔ B. This is the order resulting from placing a copy of A adjacent to a copy of B, side-by-side, forming a combined order with no instances of the order relation between the two parts.

If A is the orange v-shaped order here and B is the yellow linear order, for example, then A ⊔ B is the combined order with all five nodes.

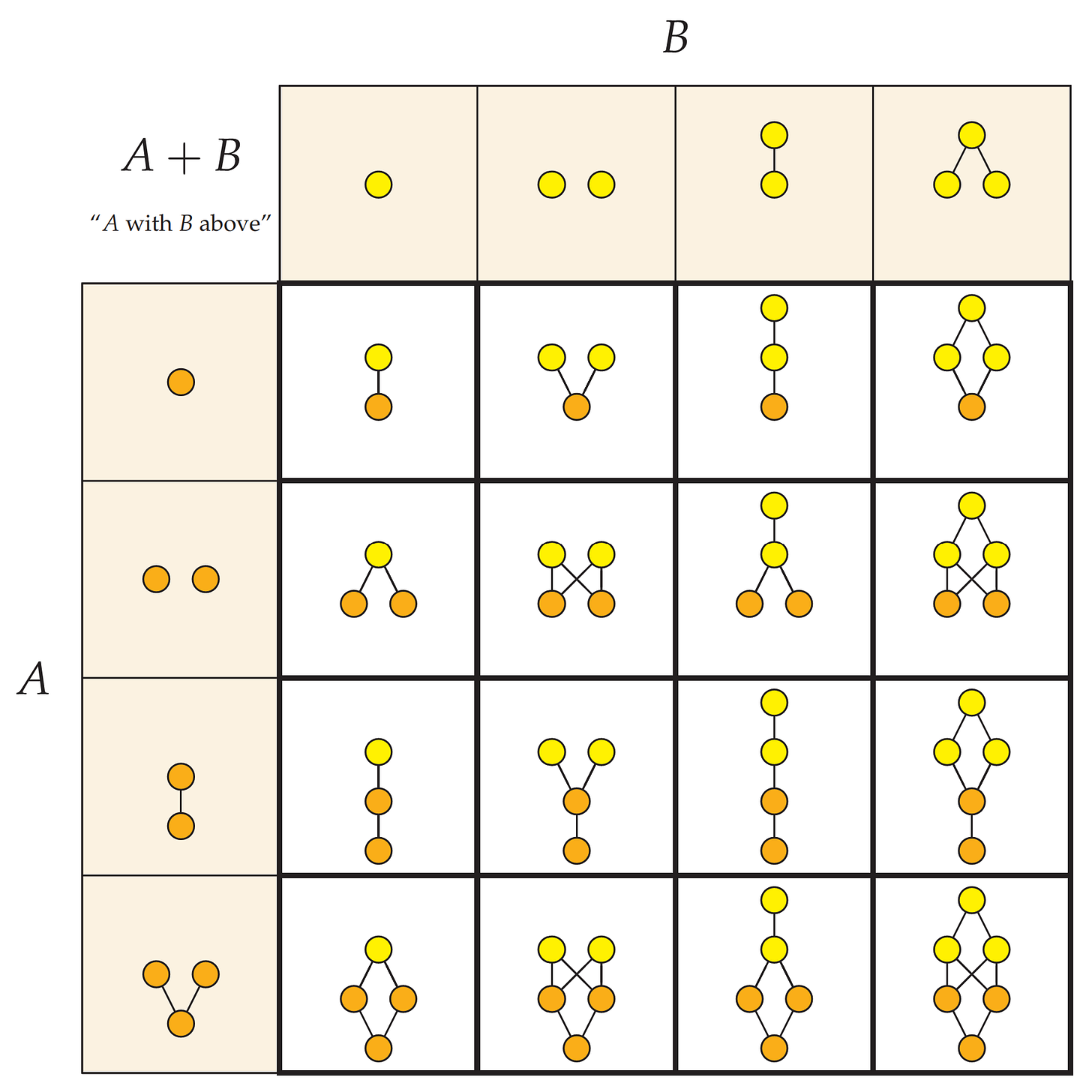
Another kind of addition is the ordered sum of two orders A + B, which is obtained by placing a copy of B above a copy of A, as indicated here by adding the orange copy of A and the yellow copy of B. We add the relation instances so that in A + B every node in the copy of A is below every node in the copy of B, and similarly with B + A.

Also shown is the sum B + A, with the summands reversed, so that we take B below and A on top. It is easy to check that the ordered sum of two orders is an order. One notices immediately, of course, that the resulting ordered sums A + B and B + A are not the same. The order A + B has a greatest element, for example, whereas B + A has two maximal elements. So the ordered sum operation on orders is not commutative. Nevertheless, we shall still call it addition. The operation, which has many useful and interesting features, goes back at least to the 19th century with Cantor, who defined the addition of well orders this way.

Pictured below is an addition table for several simple finite orders. The choices for A appear down the left side and those for B at the top, with the corresponding sum A + B displayed in each cell of the matrix accordingly.

We can combine the two order addition operations, forming a variety of other orders this way: