Boolean-algebra logic
Multi-valued logics realizing exactly the classical logic validities
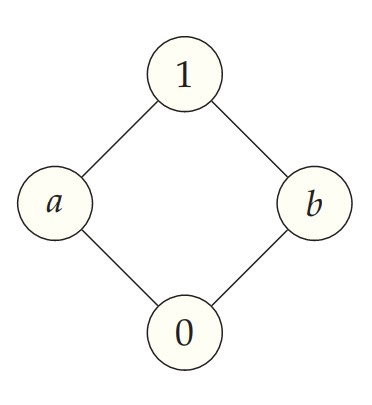
Consider the four-valued logic pictured here, which we denote by 𝟚2 because it will turn out to be an instance of the more general power-set logics 𝟚X we shall consider shortly.
Although multi-valued, this logic exhibits a strong affinity with classical logic—far more so than other multi-valued logics we have considered, including Kleene logic, Łukasiewicz logic and fuzzy logic. For instance, we shall prove that the validities of this logic are exactly the classical validities, which we saw earlier is not true for those other multi-valued logics.
In this four-valued logic 𝟚2, we have the absolutely false value 0, the absolutely true value 1, and two intermediate truth values a and b. The core idea of this logic is that the intermediate truth values a and b are each shades of truth, insufficient on their own for full truth, yet together they combine to make full truth. In short, the intermediate truth values are complementary. Specifically, in this logic we define a ∧ b = 0 and a ∨ b = 1, as well as ¬a = b and ¬b = a. More generally, in this logic it happens that x ∧ y is always the greatest lower bound of x and y in the order that is pictured, and x ∨ y is the least upper bound. One can then define → and ↔ in turn so as to realize the identities
and
We might notice straight away that this logic fulfills the law of excluded middle—that is, p ∨ ¬p = 1 for every p, a fact that can be checked by considering each of the four possible truth values for p in turn. This is interesting because p ∨ ¬p is a classical validity that was not fully valid in Kleene logic and the other multi-valued logics we considered earlier, yet it is valid in this logic. What exactly are the validities of this logic? We say that φ(p0,...,pn) is a tautology in this logic, if the truth value is always 1, regardless of the assignments of value to the variables pi.
Theorem. A propositional assertion φ in the language of propositional logic is a tautology in the four-valued logic 𝟚2 if and only if it is a tautology in classical logic.
Proof. Let us give the argument.
Keep reading with a 7-day free trial
Subscribe to Infinitely More to keep reading this post and get 7 days of free access to the full post archives.