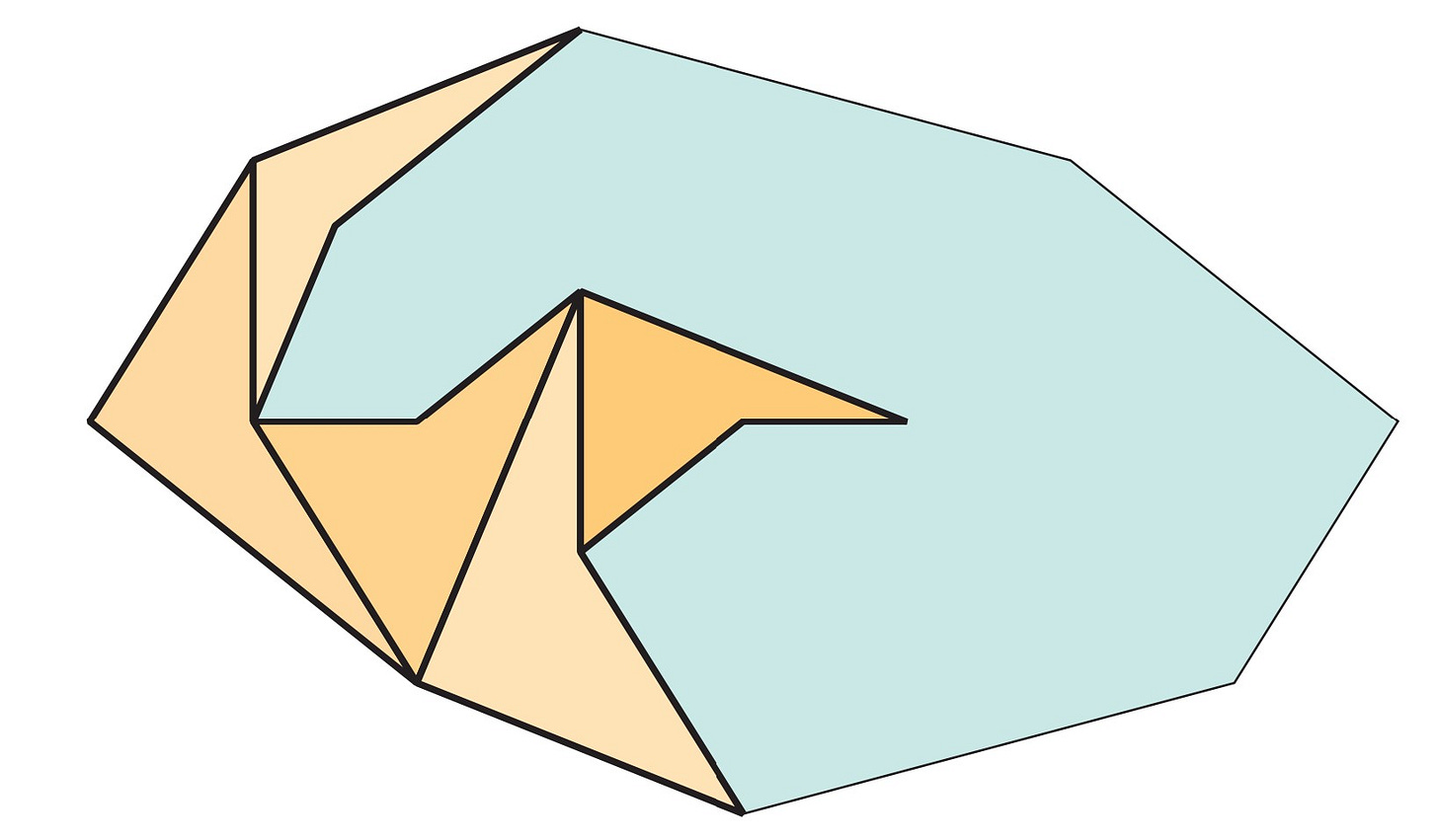
Boomerang tilings

Can you tile a convex polygon with boomerangs? Let's find out.

Let's define a boomerang as a nonconvex quadrilateral, like these:

The question I should like to consider is the following:

Question. Can we tile a convex polygon with finitely many boomerangs?

Here we have begun to tile the green convex polygon with boomerangs.

Can we complete this tiling? Give it a try!

Interlude

Did you find a completion of this tiling with boomerangs? It wasn't so easy, was it? I expect that you will likely have found it challenging to complete this particular tiling. If indeed you had, would that have been a reason to think that there is no such tiling?

Well, the difficulty of continuing any particular tiling, of course, won't seem necessarily to help us show that no convex polygon at all can be tiled by boomerangs, since perhaps we hadn't started the tiling correctly in this instance—we might have already spoiled things by starting out wrongly—or perhaps the polygon needs to have a certain number of sides or something. To answer the question negatively, what we need is some kind of general argument providing a reason why there can be no such tiling of any convex polygon with finitely many boomerangs.

When I was a graduate student, which was long before the era of MathOverflow or math.stackexchange, we had a bulletin board in the common mail room, upon which people would post mathematical puzzles and challenges to the members of the Berkeley math community. Others would post various answers or answer attempts, until in time the problem was solved.

One morning, I came into the department and found the puzzle that is the focus of this essay—can you tile a convex polygon with boomerangs? Soon various solution attempts were posted and then criticized, until by the end of the day we had found a solution. So let me tell you about it and also about several generalizations of the puzzle.