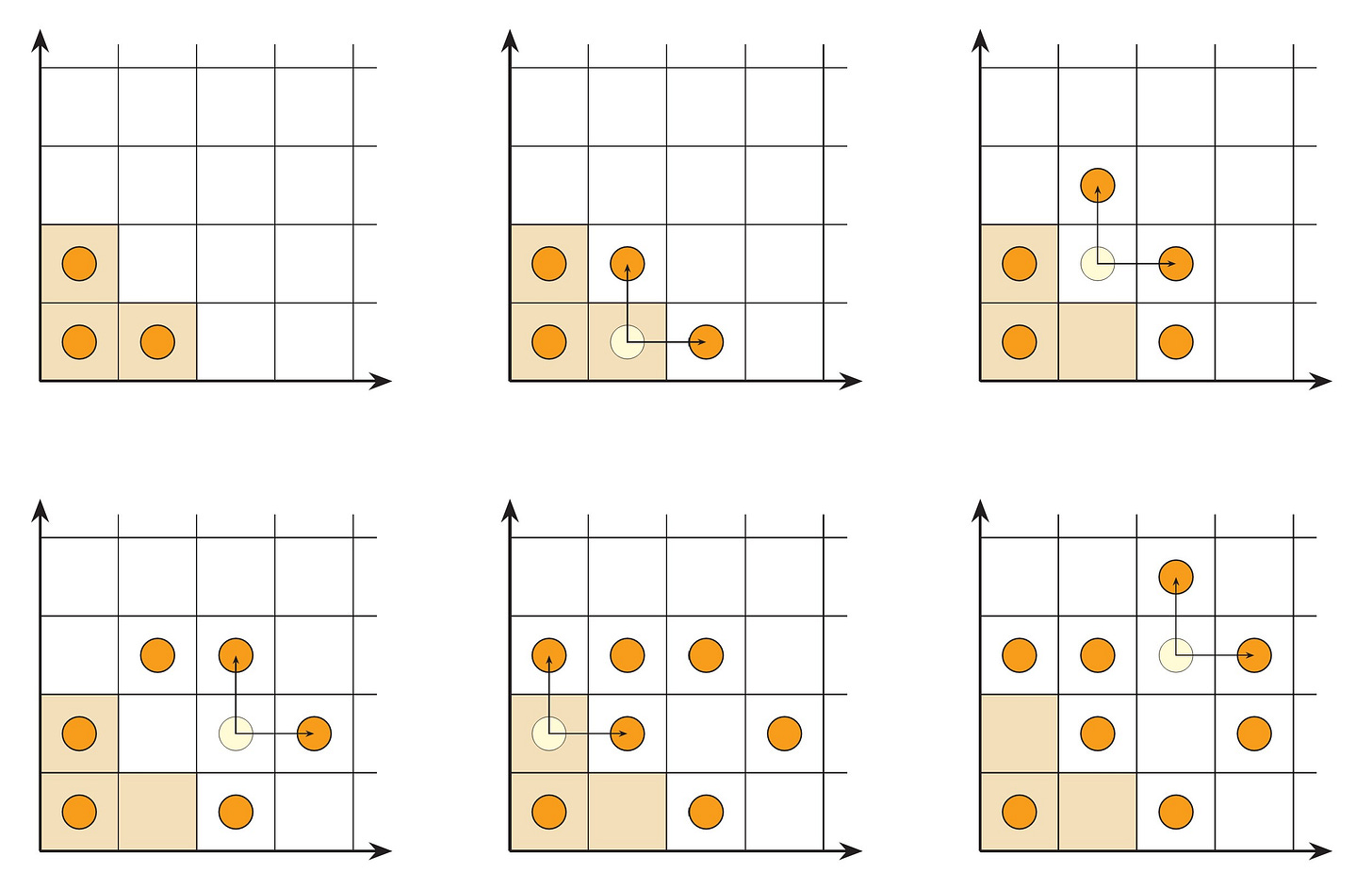
Consider next the game Escape! We have three stones in the corner of an infinite quarter plane of squares. The rule of movement is that you can select any stone you like, and it will split into two stones, one moving to the square above and one moving to the square to the right of where it had been. The move is allowed only when both of those squares are empty, so that they may accept the new stones. The goal is to vacate the shaded L-shaped region at the origin.
Can you vacate the shaded corner area? Please give it a try. One can make a good start, but then the outer stones begin to block one's path. You have to move these other stones out of the way to make room. Is it possible to get all three stones out of the corner? I have provided an online interactive version of the game, for trying out strategies and ideas, at this link, and see also my blog post at this link.
Interlude
This is a brief excerpt from chapter 5 of my book Proof and the Art of Mathematics, an introduction to the art and craft of proof-writing for aspiring mathematicians who want to learn how to write proofs. The book is filled with compelling mathematical statements having interesting elementary proofs.
Proof and the Art of Mathematics has been awarded the 2024 Daniel Solow Author’s Award by the Mathematical Association of America, awarded for outstanding and impactful contributions to mathematics education.
Did you succeed? Perhaps one begins to think that it is impossible. But how could one ever prove such a thing?
Theorem. It is impossible to make moves in the Escape! game so as to vacate the shaded corner region.
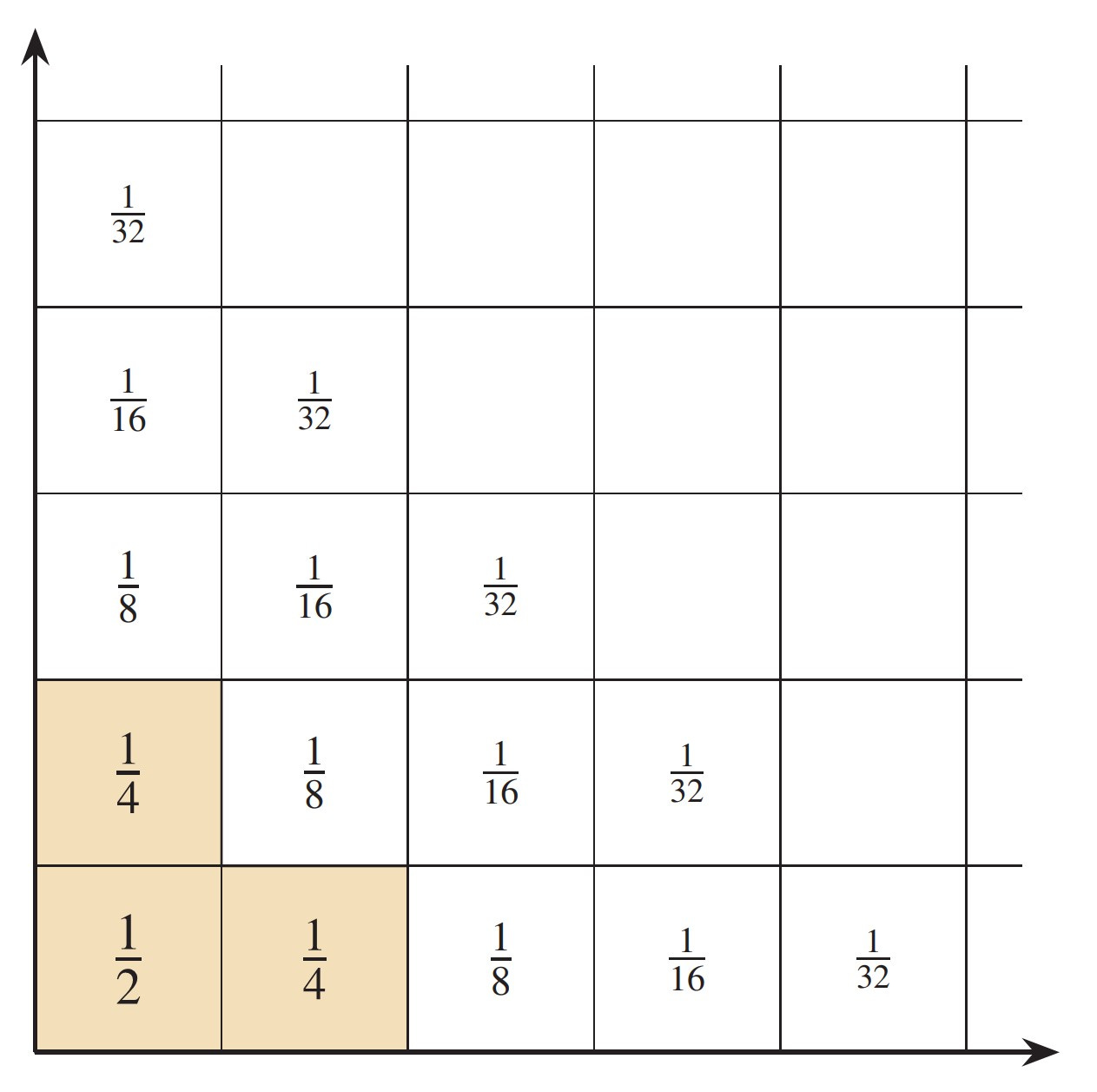
Proof: Let us assign weights to the squares in the lattice according to the following pattern: We give the corner square weight 1/2, the next diagonal of squares 1/4 each, and then 1/8, and so on throughout the whole playing board. Every square gets a corresponding weight according to the indicated pattern.
The weights are specifically arranged so that making a move in the game preserves the total weight of the occupied squares. That is, the total weight of the occupied squares is invariant as one makes moves, because moving a stone with weight 1/2k will create two stones of weight 1/2k+1, which adds up to the same. Since the original three stones have total weight
it follows that the total weight remains 1 after every move in the game. Meanwhile, let us consider the total weight of all the squares on the board. If you consider the bottom row only, the weights add to
which is the geometric series with sum 1. The next row has total weight
which adds to 1/2. And the next adds to 1/4 and so on. So the total weight of all the squares on the board is
which is 2. This leaves a total weight of 1 for the unshaded squares. The subtle conclusion is that after any finite number of moves, only finitely many of those other squares are occupied, and so some of them remain empty. So after only finitely many moves, the total weight of the occupied squares off the original L-shape is strictly less than 1. Since the total weight of all the occupied squares is exactly 1, this means that the L-shape has not been vacated. So it is impossible to vacate the original L-shape in finitely many moves. □
From chapter’s end:
Mathematical Habits
Make conjectures.
Use your mathematical insight, based on examples or suggestive reasoning, to guess the answer to a mathematical question or the mathematical fact that would explain a given mathematical phenomenon. Test your conjecture by checking whether it is consistent with known facts or examples. Try to prove your conjecture.
Exercises
12. In the Escape! game, is it possible to fill as much as desired of the plane outside of the original L-shape? For example, can one make sure for any given n that all squares in the n × n square, except possibly the original L-shape, have a stone?
13. Consider a version of the Escape! game on a finite n × n board, modifying the rules so that stones that would have been placed outside this region are simply not placed. For which values of n can you vacate the yellow corner? For which values of n can you vacate the entire board?
14. Show that in the n × n version of Escape!, you cannot lose: every sequence of legal moves leads eventually to a completely vacated board. [Hint: Show first that a nonempty board always has a legal move; next, show by induction from the lower left that every square can be activated only finitely many times. So there is no infinite play, and therefore the board must become empty at a finite stage of play.]
15. (Challenge) Show that the number of steps to vacate the n × n board does not depend on the particular sequence of moves that are made. The game always ends with an empty board in exactly the same number of steps regardless of how the plays are made.
Credits. The Escape! game is due to Maxim Kontsevich and was discussed on the Numberphile video series at this link.