The infinite subway—a full range of paradox

The second in a series of essays on the infinite subway paradox, in which we explore the full range of paradoxical behavior

We introduced the infinite subway paradox in last week’s essay, and in this essay I should like to explore the matter more fully, aiming ultimately to provide a necessary and sufficient condition on the finite disembarkment and embarkment counts that allow for a given arrival count at the limit station.

We are discussing the subway system of the city of Infinitopolis, where the trains begin each morning at the downtown terminal, station 0, and proceed uptown to station 1, station 2, station 3, and so forth, eventually arriving at the uptown terminus, station ω.

We saw in the earlier essay how it could happen that the train is picking up increasingly huge crowds at every finite station, with only one passenger disembarking each time, and yet the train arrives completely empty at the limit station. We also saw, however, how it can happen with exactly the same counts at the finite stations, that the train is totally packed in the limit. It depends not just on the counts, but on the particular details of the schedule of passenger itineraries. What is the range of possibility? Which patterns of passenger counts are possible? Which are impossible? That is what we shall figure out today.

Which patterns are possible?

I find it interesting to consider the question of which patterns of embarking and disembarking are possible on the infinite subway. For example, if we have a sequence of finite embarking and disembarking numbers at the finite stations, how many passengers could there be in general at station ω?

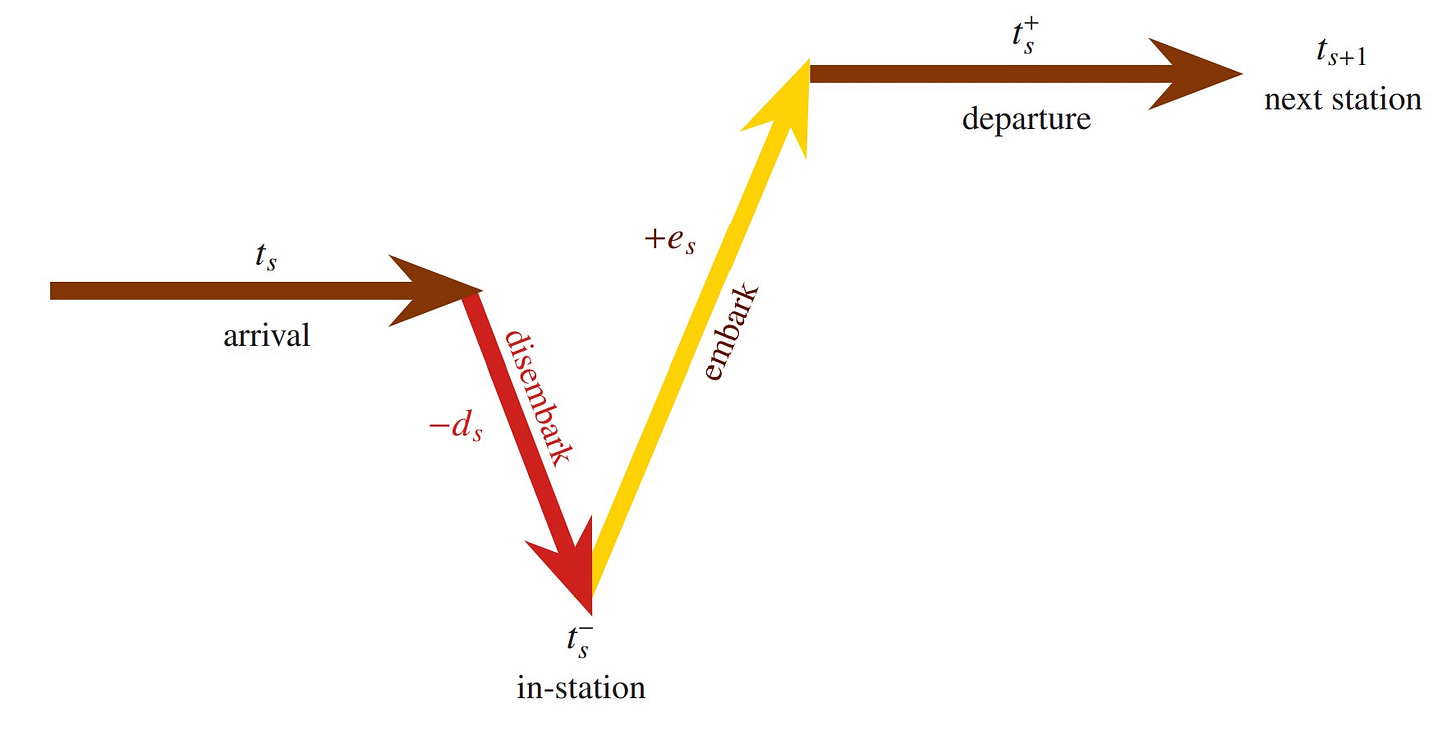
To be clear, as every New Yorker knows (while tourists, alas, too often do not), the proper order of events at any train station is that the train pulls in, passengers get off, and then other passengers get on. A passenger is on the train when arriving at a given station, if they had boarded the train at an earlier station and have not disembarked. Let us also assume that once a passenger disembarks a train, they do not reboard the same train.

Some notation and terminology will help clarify the discussion, so let me refer to the arrival passenger count t_s, which is the number of passengers on board the train when it is pulling into station s. Having arrived, the disembarkment passenger count d_s is the number of passengers disembarking, that is, who get off the train at this station. After this, the in-station passenger count t_s^- is the number of passengers remaining on the train in the station. And then the embarkment count e_s is the number of passengers getting on the train, with the resulting departure passenger count t_s⁺ being the number of passengers on board as the train departs. This is, of course, the same as the incoming passenger count t_s+1 at the next station, and in this sense we don't really need the notation t_s⁺.