Infinite Sudoku

Shall we play the Sudoku game? Starting from an empty board, we take turns placing numbers, always conforming with the Sudoku condition. Who wins? And what about infinite Sudoku?

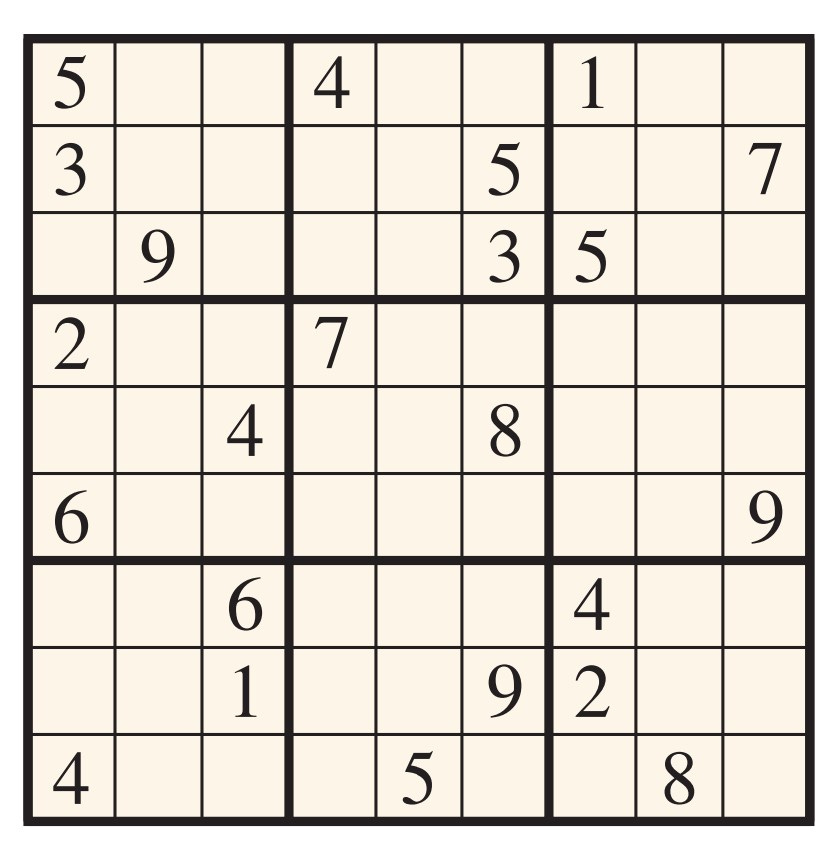
Probably most of my readers are familiar with the popular Sudoku puzzles, in which one seeks to complete the entries of a 9 × 9 square with the digits 1 though 9 in such a way that every row, every column, and each of the principal 3 × 3 subsquares uses each digit exactly once. One such puzzle is shown here—can you complete it?

A proper Sudoku puzzle contains a minimal set of clues, a partial solution, which has a unique Sudoku completion. In short, every proper Sudoku puzzle has exactly one correct answer.

The Sudoku game

Sudoku puzzles, of course, are generally a solitary activity, a puzzle meant to be solved by one person. Let me tell you, however, about a two-player variation, the Sudoku game.

We start with a completely empty Sudoku board, vacant of numbers, and then take turns placing numbers.

But these numbers must never explicitly violate the Sudoku condition, that is, numbers must never repeat on any row, column or principal sub-board. The first player who has no legal move loses.

The game is therefore not about building a global Sudoku solution, since a move can be legal in this game even when it is not part of any global Sudoku solution, provided only that it doesn't yet explicitly violate the Sudoku conditions. Rather, the Sudoku game is about trying to trap your opponent in a position that does not yet explicitly violate the Sudoku condition, but which cannot be further extended.

Who will win the game?

Interlude

The game makes sense not just on the 9 × 9 board, but actually on any n² × n² board. For example, we can play 16 × 16 Sudoku, or 125 × 125 Sudoku. Later, we shall discuss that the game can be naturally extended to the case of rectangularly symmetric boards of size (n × k) × (k × n), with rectangular subboards, such as 6×6 = (2×3)×(3×2).

And we shall forthwith move on to the infinite Sudoku games. Do you fancy a game of Sudoku on the integer-by-integer grid of integer-by-integer grids? How about the (ℝ×ℝ)×(ℝ×ℝ) Sudoku board? And higher cardinals?