Infinitesimals revisited
How infinitesimal calculus became rigorous
Please enjoy this free extended excerpt from Lectures on the Philosophy of Mathematics, published with MIT Press 2021, an introduction to the philosophy of mathematics with an approach often grounded in mathematics and motivated organically by mathematical inquiry and practice. This book was used as the basis of my lecture series on the philosophy of mathematics at Oxford University.
Infinitesimals revisited
For the final theme of this chapter, let us return to the infinitesimals. Despite the problematic foundations and Berkeley's criticisms, it will be good to keep in mind that the infinitesimal conception was actually extremely fruitful and led to many robust mathematical insights, including all the foundational results of calculus. Mathematicians today routinely approach problems in calculus and differential equations essentially by considering the effects of infinitesimal changes in the input to a function or system.
For example, to compute the volume of a solid of revolution y = f(x) about the x-axis, it is routine to imagine slicing the volume into infinitesimally thin disks. The disk at x has radius f(x) and infinitesimal thickness dx (hence volume πf(x)2dx), and so the total volume between a and b, therefore, is
Another example arises when one seeks to compute the length of the curve traced by a smooth function y = f(x). One typically imagines cutting it into infinitesimal pieces and observing that each tiny piece is the hypotenuse ds of a triangle with infinitesimal legs dx and dy. So by an infinitesimal instance of the Pythagorean theorem, we see
from which one “factors out” dx, obtaining
and therefore the total length of the curve is given by
Thus, one should not have a cartoon understanding of developments in early calculus, imagining that it was all bumbling nonsense working with the ghosts of departed quantities. On the contrary, it was a time of enormous mathematical progress and deep insights of enduring strength. Perhaps this situation gives a philosopher pause when contemplating the significance of foundational issues for mathematical progress — must one have sound foundations in order to advance mathematical knowledge? Apparently not. Nevertheless, the resolution of the problematic foundations with epsilon-delta methods did enable a far more sophisticated mathematical analysis, leading to further huge mathematical developments and progress. It was definitely valuable to have finally fixed the foundations.
Nonstandard analysis and the hyperreal numbers
What an astounding development it must have been in 1961, when Abraham Robinson introduced his theory of nonstandard analysis. This theory, arising from ideas in mathematical logic and based on what are now called the hyperreal numbers ℝ*, provides a rigorous method of handling infinitesimals, having many parallels to the early work in calculus. I look upon this development as a kind of joke that mathematical reality has played on both the history and philosophy of mathematics.
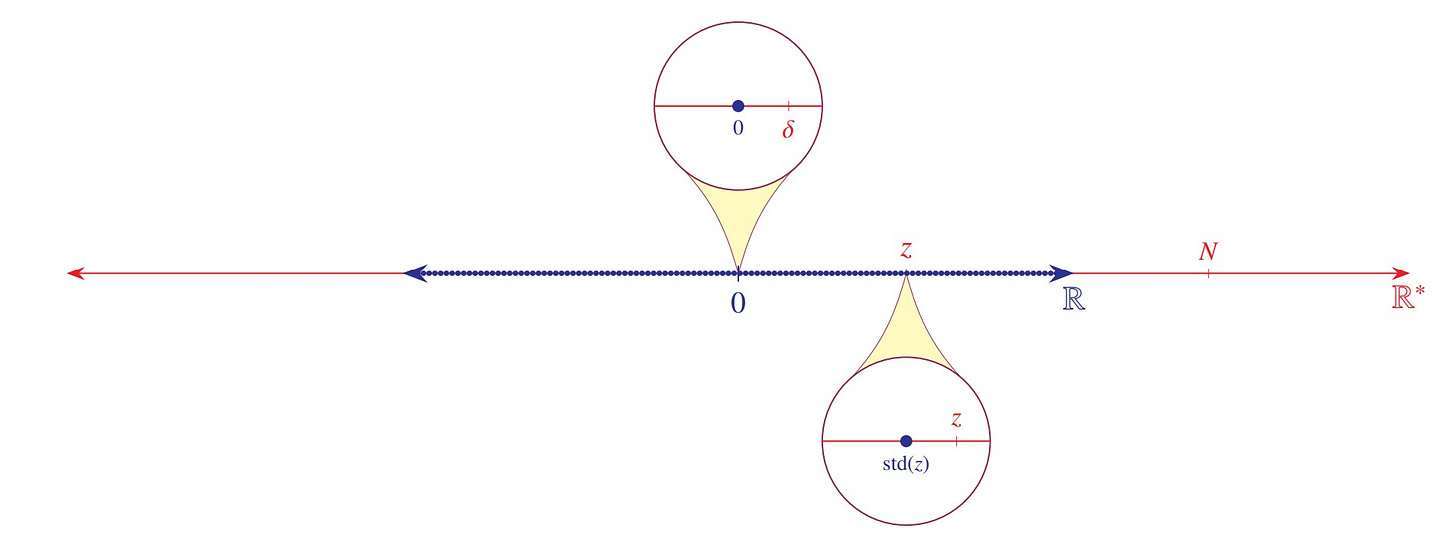
The way it works is as follows. The hyperreal number system ℝ* is an ordered field extending the real numbers, but having new infinite and infinitesimal numbers. In the figure, the real number line—meaning all of it, the entire real number line—is indicated in blue. The hyperreal number line, indicated in red, thus extends strictly beyond the end of the real number line. It may be difficult to imagine at first, but indeed this is what the construction of the hyperreal numbers produces. The hyperreal number N indicated in the figure, for example, is larger than every real number, and the number δ is positive, being strictly larger than 0 but smaller than every positive real number. One could imagine that δ = 1/N, since the reciprocal of an infinite number will be infinitesimal and conversely.
Every real number is surrounded by a neighborhood of those hyperreal numbers infinitesimally close to it, and so if one were to zoom in on a real number in the hyperreal numbers, one would ultimately find a window containing only that real number and the hyperreal numbers infinitely close to it. Every hyperreal z that is bounded by standard real numbers is infinitesimally close to a unique standard real number, called the standard part of z and denoted as std(z), as indicated in the figure.
Part of what makes the hyperreal numbers attractive for nonstandard analysis is their further remarkable property that any statement in the formal language of analysis that is true for the real numbers ℝ is also true for the hyperreal numbers ℝ*. The transfer principle asserts that every real number a and function f on the real numbers have nonstandard counterparts a* and f* in the hyperreal numbers, such that any assertion φ(a, f ) about a and f that is true in the real numbers ℝ is also true of the counterparts φ(a*, f *) in the hyperreal numbers ℝ*. Thus, the real numbers have an elementary embedding a ↦ a* into the hyperreal numbers ℝ ≺ ℝ*.
Because of the transfer principle, we know exactly what kinds of arithmetic and algebraic operations are allowed in the hyperreal numbers—they are the same as those allowed in the real number system. Because of the transfer principle, we will have concepts of infinite integers, infinite prime numbers, infinite powers of 2, and so on, and we can divide an interval in the real numbers into infinitely many subintervals of equal infinitesimal length. These are exactly the kinds of things that one wants to do in calculus, and nonstandard analysis provides a rigorous foundation for it.
Calculus in nonstandard analysis
Let us illustrate this by explaining how the derivative is treated in nonstandard analysis. One computes the derivative of a function f by using an infinitesimal hyperreal number, without any limit process or epsilon-delta arguments. To find the derivative of f(x) = x2, for example, let δ be a positive infinitesimal hyperreal. We compute the rate-of-change quotient over the interval from x to x + δ,
with the same algebraic steps as performed earlier, and then simply take the standard part of the result, arriving at
Thus, the derivative of x2 is 2x. The use of the standard-part operation in effect formalizes how one can correctly treat infinitesimals—it explains exactly how the ghosts depart! Thus, nonstandard analysis enables a fully rigorous use of infinitesimals.
Nonstandard analysis has now grown into a mature theory, providing an alternative conception parallel to the classical theory. There are several philosophical perspectives one might naturally adopt when undertaking work in nonstandard analysis, which I would like now to explain. Some of this material is technical, however, and so readers not familiar with ultrapowers, for example, might simply skip over it.
Classical model-construction perspective
In this approach, one thinks of the nonstandard universe as the result of an explicit construction, such as an ultrapower construction. In the most basic instance, one has the standard real number field structure ⟨ℝ, +, ·, 0, 1, ℤ⟩, and you perform the ultrapower construction with respect to a fixed nonprincipal ultrafilter U on the natural numbers (or on some other set if this were desirable). The ultrapower structure ℝ* = ℝℕ/U is then taken as a conception of the hyperreal numbers, an ordered non-Archimedean field, which therefore has infinitesimal elements.
In time, however, one is led to want more structure in the pre-ultrapower model, so as to be able to express more ideas, which will each have nonstandard counterparts. One will have constants for every real number, a predicate for the integers ℤ, or indeed for every subset of ℝ, and a function symbol for every function on the real numbers, and so on. In this way, one gets the nonstandard analogue z* of every real number z, the set of nonstandard integers ℤ*, and nonstandard analogues f * for every function f on the real numbers, and so on. Before long, one also wants nonstandard analogues of the power set P(ℝ) and higher iterates. In the end, what one realizes is that one might as well take the ultrapower of the entire set-theoretic universe V → Vω/U, which amounts to doing nonstandard analysis with second-order logic, third- order, and indeed α-order for every ordinal α. One then has the copy of the standard universe V inside the nonstandard realm V*, which one analyzes and understands by means of the ultrapower construction itself.
Some applications of nonstandard analysis have required one to take not just a single ultrapower, but an iterated ultrapower construction along a linear order. Such an ultrapower construction gives rise to many levels of nonstandardness, and this is sometimes useful. Ultimately, as one adds additional construction methods, this amounts just to adopting all model theory as one's toolkit. One will want to employ advanced saturation properties, or embeddings, or the standard system, and so on. There is a well developed theory of models of arithmetic that uses quite advanced methods. To give a sample consequence of saturation, every infinite graph, no matter how large, arises as an induced subgraph of a nonstandard-finite graph in every sufficiently saturated model of nonstandard analysis. This sometimes can allow you to undertake finitary constructions with infinite graphs, with the cost being a move to the nonstandard context.
Axiomatic approach
Most applications of nonstandard analysis, however, do not rely on the details of the ultrapower or iterated ultrapower constructions, and so it is often thought worthwhile to isolate the general principles that make the nonstandard arguments succeed. Thus, one writes down the axioms of the situation. In the basic case, one has the standard structure ℝ, and so on, perhaps with constants for every real number (and for all subsets and functions in the higher-order cases), with a map to the nonstandard structure ℝ*, so that every real number a has its nonstandard version a* and every function f on the real numbers has its nonstandard version f *. Typically, the main axioms would include the transfer principle, which asserts that any property expressible in the language of the original structure holds in the standard universe exactly when it holds of the nonstandard analogues of those objects in the nonstandard realm. The transfer principle amounts precisely to the elementarity of the map a ↦ a* from standard objects to their nonstandard analogues. One often also wants a saturation principle, expressing that any sufficiently realizable type is actually realized in the nonstandard model, and this just axiomatizes the saturation properties of the ultrapower. Sometimes one wants more saturation than one would get from an ultrapower on the natural numbers, but one can still achieve this by larger ultrapowers or other model-theoretic methods.
Essentially the same axiomatic approach works with the higher-order case, where one has a nonstandard version of every set-theoretic object, and a map V → V*, with nonstandard structures of any order. And similarly, one can axiomatize the features that one wants to use in the iterated ultrapower case, with various levels of standardness.
“The” hyperreal numbers?
As with most mathematical situations where one has both a construction and an axiomatic framework, it is usually thought better to argue from the axioms, when possible, than to use details of the construction. And most applications of nonstandard analysis that I have seen can be undertaken using only the usual nonstandardness axioms. A major drawback of the axiomatic approach to nonstandard analysis, however, is that the axiomatization is not categorical. There is no unique mathematical structure fulfilling the hyperreal axioms, and no structure that is “the” hyperreal numbers up to isomorphism. Rather, we have many candidate structures for the hyperreal numbers, of various cardinalities; some of them extend one another, and all of them satisfy the axioms, but they are not all isomorphic.
For this reason, and despite the common usage that one frequently sees, it seems incorrect, and ultimately not meaningful, to refer to “the” hyperreal numbers, even from a structuralist perspective. The situation is totally unlike that of the natural numbers, the integers, the real numbers, and the complex numbers, where we do have categorical characterizations. To be sure, the structuralist faces challenges with the use of singular terms even in those cases (challenges we discussed in chapter 1), but the situation is far worse with the hyperreal numbers. Even if we are entitled to use singular terms for the natural numbers and the real numbers, with perhaps some kind of structuralist explanation as to what this means, nevertheless those structuralist explanations will fail completely with the hyperreal numbers, simply because there is no unique structure that the axioms identify. We just do not seem entitled, in any robust sense, to make a singular reference to the hyperreal numbers.
And yet, one does find abundant references to “the” hyperreal numbers in the literature. My explanation for why this has not caused a fundamental problem is that for the purposes of nonstandard analysis, that is, for the goal of establishing truths in calculus about the real numbers by means of the nonstandard real numbers, the nonisomorphic differences between the various hyperreal structures simply happen not to be relevant. All these structures are non-Archimedean ordered fields with the transfer principle, and it happens that these properties alone suffice for the applications of these fields that are undertaken. In this sense, it is as though one fixes a particular nonstandard field ℝ*—and for the applications considered, it does not matter much which one—and then reference to “the” hyperreal numbers simply refer to that particular ℝ* that has been fixed. It is as though the mathematicians are implementing Stewart Shapiro's disguised bound quantifiers, but without a categoricity result.
I wonder whether this lack of categoricity may explain the hesitancy of some mathematicians to study nonstandard analysis; it prevents one from adopting a straightforward structuralist attitude toward the hyperreal numbers, and it tends to push one back to the model-theoretic approach, which more accurately conveys the complexity of the situation.
Meanwhile, we do have a categoricity result for the surreal numbers, which form a nonstandard ordered field of proper class size, one that is saturated in the model-theoretic sense—as in, every set-sized cut is filled. In the standard second-order set theories such as Gödel- Bernays set theory with the principle of global choice (a class well-ordering of the universe) or Kelley-Morse set theory, one can prove that all such ordered fields are isomorphic. This is a sense in which “the hyperreal numbers” might reasonably be given meaning by taking it to refer to the surreal numbers, at the cost of dealing with a proper class structure.
Radical nonstandardness perspective
This perspective on nonstandard analysis involves an enormous foundational change in one's mathematical ontology. Namely, from this perspective, rather than thinking of the standard structures as having analogues inside a nonstandard world, one instead thinks of the nonstandard world as the “real” world, with a “standardness” predicate picking out parts of it. On this approach, one views the real numbers as including both infinite and infinitesimal real numbers, and one can say when and whether two finite real numbers have the same standard part, and so on. With this perspective, we think of the “real” real numbers as what from the other perspective would be the nonstandard real numbers, and then we have a predicate on that, which amounts to the range of the star map in the other approach. So some real numbers are standard, some functions are standard, and so on.
In an argument involving finite combinatorics, for example, someone with this perspective might casually say, “Let N be an infinite integer” or “Consider an infinitesimal rational number.” (One of my New York colleagues sometimes talks this way.) That way of speaking may seem alien for someone not used to this perspective, but for those that adopt it, it is productive. These practitioners have drunk deeply of the nonstandardness wine; they have moved wholly into the nonstandard realm — a new plane of existence.
Extreme versions of this idea adopt many levels of standardness and nonstandardness, extended to all orders. Karel Hrbacek (1979, 2009) has a well developed theory like this for nonstandard set theory, with an infinitely deep hierarchy of levels of standardness. There is no fully “standard” realm according to this perspective. In Hrbacek's system, one does not start with a standard universe and go up to the nonstandard universe, but rather, one starts with the full universe (which is fundamentally nonstandard) and goes down to deeper and deeper levels of standardness. Every model of ZFC, he proved, is the standard universe inside another model of the nonstandard set theories he considers.
Translating between nonstandard and classical perspectives
Ultimately, my view is that the choice between the three perspectives I have described is a matter of taste, and any argument that can be formulated in one of the perspectives has analogues in the others. In this sense, there seems to be little at stake, mathematically, between the perspectives. And yet, as I argued in section 1.16, divergent philosophical views can lead one toward different mathematical questions and different mathematical research efforts.
One can usually translate arguments not only amongst the perspectives of nonstandard analysis, but also between the nonstandard realm and the classical epsilon-delta methods. Terence Tao (2007) has described the methods of nonstandard analysis as providing a smooth way to manage one's ε arguments. One might say, “This δ is smaller than anything defined using that ε.” It is a convenient way to undertake error estimation. Tao similarly points out how ultrafilters can be utilized in an argument as a simple way to manage one's estimates; if one knows separately that for each of the objects a, b, and c, there is a large measure (with respect to the ultrafilter) of associated witnesses, then one can also find a large measure of witnesses working with all three of them.
For some real analysts, however, it is precisely the lack of familiarity with ultrafilters or other concepts from mathematical logic that prevents them from appreciating the nonstandard methods. In this sense, the preference for or against nonstandard analysis appears to be in part a matter of cultural upbringing.
H. Jerome Keisler wrote an introductory calculus textbook, Elementary Calculus: An Infinitesimal Approach (1976), intended for first-year university students, based on the ideas of nonstandard analysis, but otherwise achieving what this genre of calculus textbook achieves. It is a typical thick volume, with worked examples on definite integrals and derivatives and optimization problems and the chain rule, and so on, all with suitable exercises for an undergraduate calculus student. It looks superficially like any of the other standard calculus textbooks used in such a calculus class. But if you peer inside Keisler's book, in the front cover alongside the usual trigonometric identities and integral formulas you will find a list of axioms concerning the interaction of infinite and infinitesimal numbers, the transfer principle, the algebra of standard parts, and so on. It is all based on nonstandard analysis and is fundamentally unlike the other calculus textbooks. The book was used for a time, successfully, in the calculus classes at the University of Wisconsin in Madison.
There is an interesting companion tale to relate concerning the politics of book reviews. Paul Halmos, editor of the Bulletin of the American Mathematical Society, requested a review of Keisler's book from Errett Bishop, who decades earlier had been his student but who was also prominently known for his constructivist views in the philosophy of mathematics—views that are deeply incompatible with the main tools of nonstandard analysis. The review was predictably negative, and it was widely criticized, notably by Martin Davis (1977), later in the same journal. In response to the review, Keisler remarked (see also Davis and Hausner, 1978), that the choice of Bishop to review the book was like “asking a teetotaler to sample wine.”
Criticism of nonstandard analysis
Alan Connes mounted a fundamental criticism of nonstandard analysis, remarking in an interview
At that time, I had been working on nonstandard analysis, but after a while I had found a catch in the theory.... The point is that as soon as you have a nonstandard number, you get a nonmeasurable set. And in Choquet's circle, having well studied the Polish school, we knew that every set you can name is measurable; so it seemed utterly doomed to failure to try to use nonstandard analysis to do physics. (Goldstern, Skandalis 2007, interview with A Connes)
What does he mean? To what is he referring? Let me explain.
“as soon as you have a nonstandard number, you get a nonmeasurable set.”
Every nonstandard natural number N gives rise to a certain notion of largeness for sets of natural numbers: a set X ⊆ ℕ is large exactly if N ∈ X*. In other words, a set X is large if it expresses a property that the nonstandard number N has. No standard finite set is large, and furthermore, the intersection of any two large sets is large and any superset of a large set is large. Thus, the collection 𝒰 of all these large sets X forms what is called a nonprincipal ultrafilter on the natural numbers. We may identify the large sets with elements of Cantor space 2ℕ, which carries a natural probability measure, the coin-flipping measure, and so 𝒰 is a subset of Cantor space.
But the point to be made now is that a nonprincipal ultrafilter cannot be measurable in Cantor space, since the full bit-flipping operation, which is measure-preserving, carries 𝒰 exactly to its complement, so 𝒰 would have to have measure 1/2 , but 𝒰 is a tail event, invariant by the operation of flipping any finite number of bits, and so by Kolmogorov's zero-one law, it must have measure 0 or 1.
“in the Polish school, ...every set you can name is measurable.”
Another way of saying that a set is easily described is to say that it lies low in the descriptive set-theoretic hierarchy, famously developed by the Polish logicians, and the lowest such sets are necessarily measurable. For example, every set in the Borel hierarchy is measurable, and the Borel context is often described as the domain of explicit mathematics.
Under stronger set-theoretic axioms, such as large cardinals or projective determinacy, the phenomenon rises to higher levels of complexity, for under these hypotheses, it follows that all sets in the projective hierarchy are Lebesgue measurable. This would include any set that you can define by quantifying over the real numbers and the integers and using any of the basic mathematical operations. Thus, any set you can name is measurable.
The essence of the Connes criticism is that one cannot construct a model of the hyperreal numbers in any concrete or explicit manner, because one would thereby be constructing explicitly a nonmeasurable set, which is impossible. Thus, nonstandard analysis is intimately wrapped up with ultrafilters and weak forms of the axiom of choice. For this reason, it seems useless so far as any real-world application in science and physics is concerned.
Continue reading more about this topic in the book:
Lectures on the Philosophy of Mathematics, MIT Press 2021