Lattices

We explore the basic theory of lattices and investigate an intriguing instance, the lattice of partitions on a given set under refinement.

For the elements of any order, we say that b is an upper bound of a to mean simply that a ≤ b, and more generally b is an upper bound of an entire set when it is an upper bound of every element of that set. The object b is the least upper bound of a set A, also known as the supremum of A and denoted b = sup(A), if b is least amongst the collection of upper bounds of A—that is, b ≤ c for any other upper bound c. The least upper bound of a pair set { a, b }, when it exists, is called the join of a and b and is denoted by a ∨ b.

And similarly for the downward-oriented dual notions. Namely, b is a lower bound of a set A if b ≤ a for every a ∈ A and it is the greatest lower bound or infimum of A, denoted b = inf(A), if it is greatest amongst the lower bounds of A. The infimum of a pair { a, b } is called the meet of a and b and is denoted by a ∧ b.

A lattice is an order relation in which every pair of elements have a least upper bound and a greatest lower bound. The two orders shown here are lattice orders—the meet a ∧ b of any two elements a and b is obtained by following the diagonals downwards towards each other until they merge, and the join a ∨ b is obtained by following diagonals upward.

Further examples abound. Every linear order is a lattice, because the join of two elements will simply be the larger of them and the meet will be the smaller of them. The set of positive integers is a lattice under divisibility n | m, since any two positive integers have a greatest common divisor and a least common multiple. Every field of sets is a lattice with respect to the subset relation, since the union of two sets a ∪ b will be their least upper bound with respect to ⊆ and the intersection a ∩ b will be their greatest lower bound. In light of the Stone Representation theorem, it follows that every Boolean algebra is a lattice, and indeed it is this fact that is the source of the notation a ∧ b and a ∨ b for lattices—the conjunction of two truth values p ∧ q is their greatest lower bound and the disjunction p ∨ q is their least upper bound.

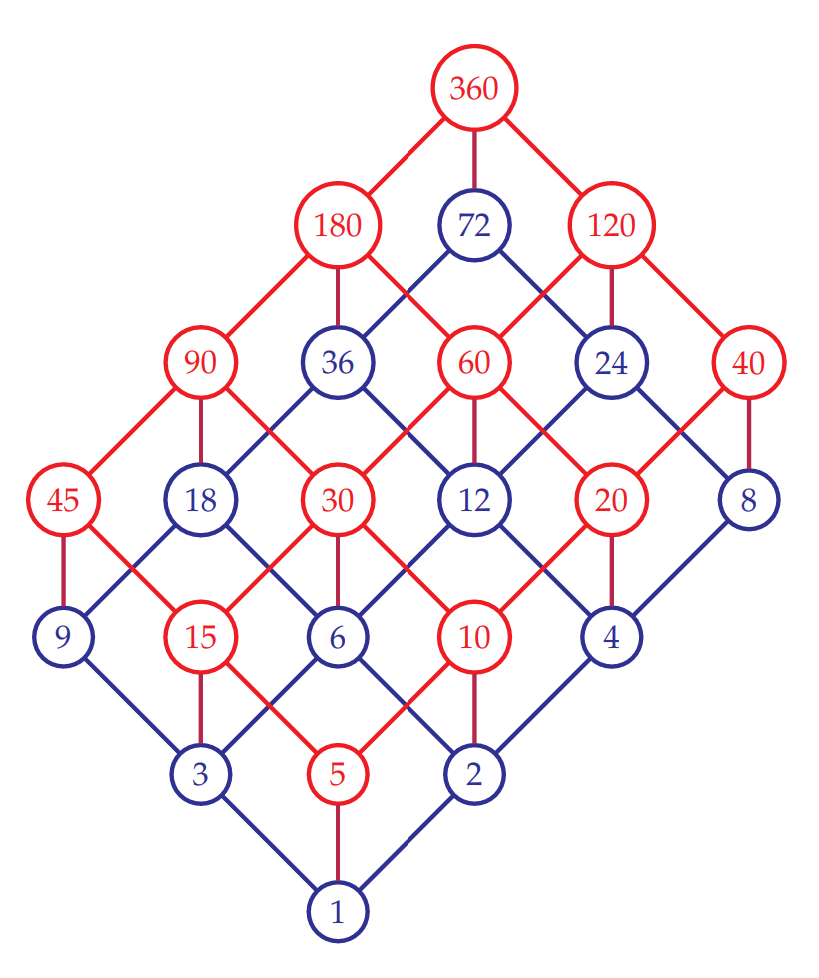
Here is the lattice of divisibility for the factors of 360. Every factor of 360 appears, and the join of any two numbers is the least common multiple and the meet is the greatest common divisor. One might notice a three-dimensional perspective aspect of this lattice—it appears as the isometric view of a 3 × 2 × 1 rectangular solid. The explanation of this is the prime factorization 360 = 2³ · 3² · 5¹, which has exponents of 3, 2, and 1. Since every factor is determined by taking some or all or none of each exponent, the lattice makes three steps in the multiplying-by-2 direction (up and right), two steps in the multiplying-by-3 direction (up and left), and one step in the multiplying-by-5 direction (straight up). Every factor is determined by the number of steps it has taken in each of those directions, like three dimensional integer coordinates. This lattice is a small part, a finite sublattice, of the entire lattice of divisibility on the positive integers.

The two simple lattices shown below play an outsized role in the theory of lattices by serving as fundamental counterexamples to what might have seemed a very natural property in lattices.