Łukasiewicz logic and supervaluation logic

Further explorations in multi-valued logic, with extraordinary truth values beyond truth and falsity.

Let us continue our explorations of multi-valued logic, entering a realm of truth beyond the two classical values of true and false. In last week’s post, we had explored Kleene logic; this time we shall investigate Łukasiewicz logic and supervaluation logic.

Łukasiewicz logic

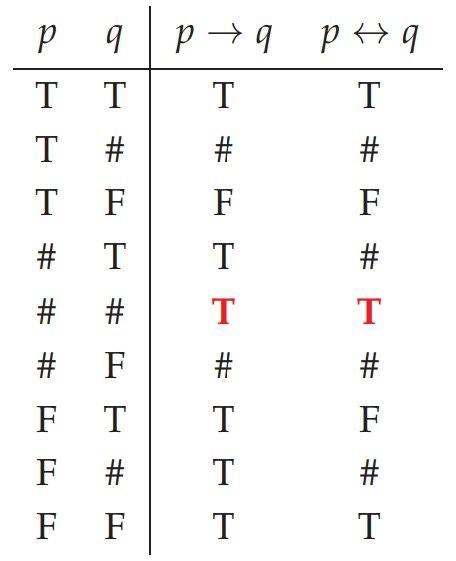
Łukasiewicz’s three-valued logic had preceeded Kleene logic, although the two are closely related. Indeed, they are identical except for their treatment of the implication p → q and a corresponding difference in the biconditional p ↔ q, which in Łukasiewicz logic are defined as in the table here.

The only change occurs in the row where p and q are both #, with the new values highlighted in boldface red. We shall write ⟦ φ ⟧^Ł for the truth valuation of φ in Łukasiewicz logic.

In contrast to Kleene logic, Łukasiewicz logic has honest tautologies, such as p → p and p ↔ p, which get value T all the way down. So the analogue of our earlier theorem for Kleene logic (showing that there are no strong tautologies) fails for Łukasiewicz logic, although it still holds in the language { ∧, ∨, ¬ }, since this fragment of Łukasiewicz logic agrees with Kleene logic.

Similarly, the Łukasiewicz analogue of the partial completeness result we proved for Kleene logic, showing that every expression in the standard language is expressible with just { ∧, ¬ } or just { ∨, ¬ }, is not true, since even with { ∧, ∨, ¬ } we cannot express the Łukasiewicz implication →, as the former are # -preserving, but the latter is not. Meanwhile, the standard connectives { ∧, ∨, →, ↔, ¬ } remain expressively incomplete in Łukasiewicz logic just as they are in Kleene logic, because these connectives are all still classical-value-preserving. Indeed, this is simply an instance of the earlier theorem we had proved for Kleene logic.

The previous analysis of smoothness, however, fails for Łukasiewicz logic in the language with →, as the Łukasiewicz implication p → q is not smooth in light of the fact that # # is close to T F, but this makes a change in the truth value from T to F. Perhaps the lack of smoothness for → can be seen as a serious drawback to the Łukasiewicz conception of implication, if we aim to interpret # as somehow intermediate between true and false—one might have expected smoothness. Yet precisely because of its lack of smoothness, the Łukasiewicz implication carries extra expressive power that Kleene logic does not: