Chaos train and monkey madness—fun with quantifiers in first-order logic
Learn the language of first-order logic by immersion in some fun logic puzzles
Enjoy this free short installment from A Panorama of Logic, my new book that I have been serializing here on Infinitely More. The book is an introduction to all aspects of logic, for philosophers, mathematicians, and computer scientists. This week we have an introduction to quantifiers, especially nested quantifiers—learn the language of first-order logic by a brief immersion in these whimsical puzzles.
I am serializing all my new books here on Infinitely More, with fresh chapters every week, and regular extended excerpts from my already published books. Subscribe now for full access to the latest posts, as well as the archives.
First-order predicate logic
We come now into the heart of logic with first-order predicate logic, providing a formal language and semantics, capable of expressing fine distinctions and shades of meaning—the subject of logic at its core is focused upon the interaction of language and meaning. The language of predicate logic is rich, able to express the concepts of essentially arbitrary kinds of mathematical structure. How remarkable it is that by studying the power and limitations of a formal language we are also so often led to mathematical insight.
Informal practice with quantifiers
Before launching into the full details of the formal language, however, let us first get some informal practice—perhaps one learns a new language best simply by immersing oneself in it. We shall put off the grammatical details and formalities until we have attained a native felicity.
The background context for assertions in predicate logic, just as in relational logic, is a fixed domain of individuals, considered as though an entire world of its own. Upon that domain, we shall have fixed relations or predicates, perhaps also functions and operations, as well as names or constants that pick out particular individuals, allowing us directly to refer to them. The quantifiers ∃ and ∀ range over the domain—to assert ∃x φ is to say “there is an x such that φ,” meaning that there is such an x to be found in the domain, and similarly ∀x φ asserts “every x has property φ,” again meaning every x in the domain. Let us illustrate.
Parenthood
Consider the parent of relation on the set of all people, the relation Pxy that holds when person x is a parent of person y. What proposition is expressed by the following assertion?
Perhaps someone suggests that it asserts “everyone has a parent.” Is that right? Well, no. If we look carefully, the statement asserts that for every person x there is a person y such that x is the parent of y. So this sentence asserts rather that “everyone is a parent.” And of course, this sentence isn't true—not everyone is a parent, since some people have not had any children. We may express the proposition “everyone has a parent,” in contrast, in the following manner:
Is this sentence true? We had said that we are considering the parent-of relation on the domain of all people, so the quantifers ∀y and ∃x range over all people and the sentence asserts that for every person y there is a person x such that x is the parent of y. If we had meant the domain of all living people, then this second sentence also would be false, since there are many people whose parents have unfortunately both passed away.
Let us therefore consider the relation instead on the domain of all people who have ever lived. You and I are both in this domain, with your parents, your grandparents, Newton, Napoleon, Aristotle, and their parents, and so on. Would it now be true that everyone has a parent in this expanded context? Perhaps this seems obvious—everyone has had a parent, right?—but let us consider the matter carefully. If you have a parent, and your parent has a parent, and they have a parent, we might reach in this way into your ancestry. But assuming there are no cycles in the parenthood relation, this would lead to an unending chain of distinct ancestors—there must have been infinitely many people!
Following your chain of ancestors into antiquity, we reach through the generations of humanity eventually to the species of homo erectus and other early homonid species. Are these individuals in the set of all people? If so, then we proceed earlier, through the early primates to the primitive mammal species, and so on. Are these people? If we delineate a personhood border at any point, then the chain of ancestors will cross it, making the statement false that for every person there is a person who is their parent. And if we do not delineate a border, then the chain of ancestors will eventually reach the most primitive life forms, an originating life form with no parent, again making the statement false. We seem obliged to admit in any case that the statement ∀y ∃x Pxy expressing the proposition “everyone has a parent” is not true when interpreted on the set of all people who have ever lived.
The gift-givers
Imagine a community of kind individuals and consider the relation Gxy which holds of individuals in that community, when person x has just made a home-made gift and given it to person y. Try to match up the formal statements below at left with the phrases at right that allude to the meaning, perhaps without expressing it exactly. Can you find the best matches?
I have started you out by noticing that the assertion ∃x ∃y Gxy expresses the proposition that in at least one instance, a person just made a home-made gift for someone—isn't that nice? Can you match the other statements?
Post your solutions to all these puzzles in the comments below!
[Note to instructor: completing these matchings and the others below often makes for a fruitful classroom activity to undertake as a group—all suggestions should come with explanation from the students.]
Chaos train
The passengers on a New York subway train are heading downtown on particular Monday morning.
Let Bxy mean “person x accidentally bumped into person y on the train, and said ‘excuse me.’ ” Find the best matching of the formal statements with their corresponding phrases.
I suggested a match for ∃x ∃y Bxy, which expresses that in at least one instance, a person x has accidentally bumped into some person y—unfortunately, it happens. Can you match the remaining assertions?
Monkey madness
Next we encounter a riotous day at the zoo.
Consider the predicate Tmbn expressing the trinary relation:
Monkey m tosses banana b to monkey n.
Let us try to match the formal statements below with the phrases that allude to the meaning, perhaps without expressing it exactly.
In these statements, we have two sorts of objects—monkeys and bananas—and each sort has its own quantifiers and variables. Quantifiers using the variables m and n range over the monkeys at the zoo, and the quantifiers using b range over the bananas there. Find the best matching of the formal assertions with the descriptive phrases. I have begun by observing that ∃m ∃b ∃n Tmbn expresses the proposition that in at least one instance, a monkey has tossed a banana to another monkey (or perhaps to himself), and so indeed there is “a banana up in the air.” Can you complete the matching?
Post your solutions in the comments below!
What’s coming up
The formal language of first-order logic
Structures in a given language signature
The semantics of truth
Theory theory
Definability
Interpretability
Model theory
Much more!
Exercises
A nice collection of exercises this week—highly recommended to gain expertise in quantifier logic. Give them all a try!
Translate the following assertion into natural language, where Pxy expresses “x is a parent of y,” and state whether the statement is likely true or false amongst the set of all living people.
Express the following assertions in the formal language of x\mathrel{L} y, meaning “x loves y.” If the assertion is ambiguous, provide multiple interpretations. Quantifiers range over all people.
Translate each of the following assertions into ordinary English, where Ax means “x is an adult,” Tx means “x is a passenger on the train,” and Sxy means “x is sitting next to y.” Please find the simplest, most natural way to say it.
Express the following assertions in the formal language of Ss, meaning “s is a station” and Dd, meaning “d is a door” (on the train), and Ods, meaning “door d opens at station s.” Quantifiers range over absolutely everything.
Suppose that students have just completed a course in applied ethics and it is time for the final exam, but perhaps not all the students have studied the readings sufficiently. Let Cxy express that “student x copied from student y on the exam.” Create a matching-phrases puzzle for the following formal statements, in the style of the monkey madness exercise, by creating a list of six pithy phrases that allude to the meaning expressed, without necessarily expressing the meaning literally. For example, one of the assertions might be about “an impressively desperate student” and regarding another, “the invigilator has left the building.” Can your fellow students solve your matching puzzle?
Express the following assertions in the formal language of x C y, meaning “x is a child of y” and W(x), meaning “x is a woman.” Quantifiers range over people.
Complete the matching for the gift-giving community.
Complete the matching for the chaos train passenger example.
Complete the matching for the monkey madness at the zoo.
Express the following assertions in the formal language of the monkey madness puzzle.
Which of the following are true in the real numbers ℝ, with the usual addition and multiplication? (Thanks to Andrej Bauer.)
Discuss the nature of “generic” assertions, such as
Do these assertions carry the meaning of ∃ or ∀? Or something else? What is the logic of generic assertions?
What does “only” mean? In fact, the word “only” is frequently misplaced or otherwise wrongly used in common parlance. Explain the differences in meaning in the following sentences.
What meaning do the following sentences express, and which are true?
Imagine a friend who had wanted to help you, but instead their actions had caused a problem, and so now the friend wants to apologize by saying one of the following sentences. What do these sentences mean, and do any of them express a suitable apologetic meaning for your friend?
Translate ∃z ∀x ∃y (x ≠ y ∧ y ≠ z) into an equivalent simple statement in plain language.
Credits
The illustrations were created by author via DALL·E and the collection is available at https://labs.openai.com/c/UEU2PFntFefdbSjVBcVvOiX7.








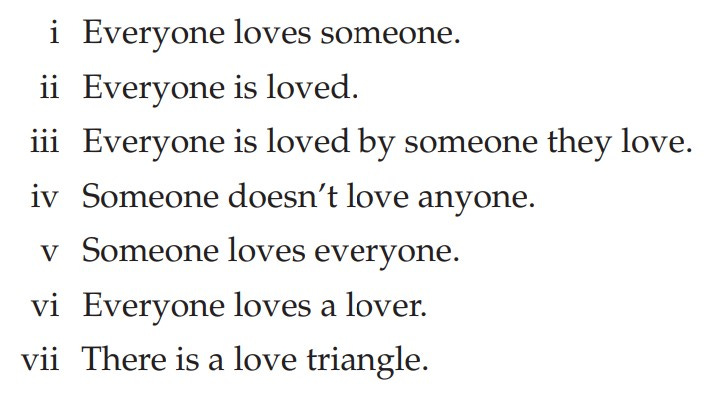
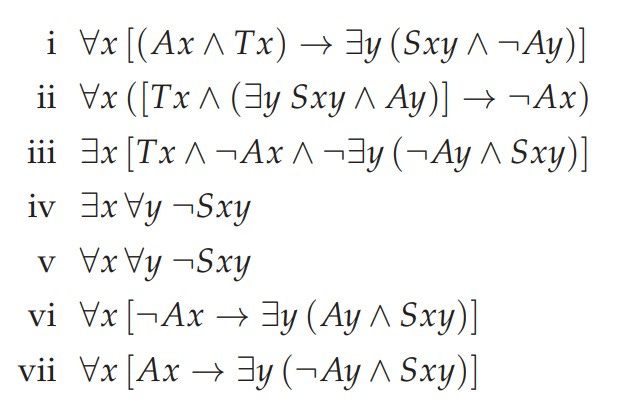

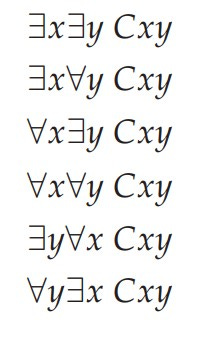


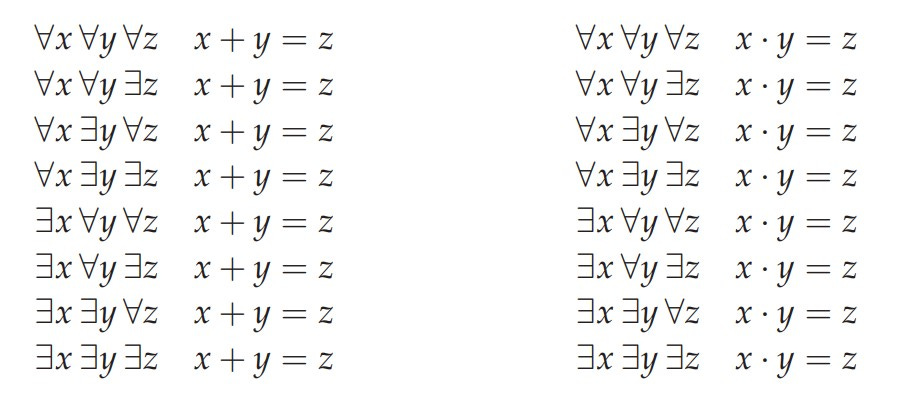




Exists y for all x Gxy -- Universally beloved. If not everyone has a parent I guess it was the egg that came first in the chicken vs egg debate.