Pointwise definability versus Leibnizian discernibility
A model is pointwise definable when every individual has a property only it has. The model is Leibnizian if distinct individuals fulfill different properties. Are these the same or different?
Definability enables our capacity for indirect reference—we may refer to an object without ever touching it or pointing at it directly, but instead picking it out by mentioning a property that only it has, a feature that distinguishes it from all other objects.
Definable elements
Specifically, an individual is definable in a structure if it satisfies a defining property, that is, if it has a property in the structure that amongst all individuals there only it has. More precisely, an individual a is definable in a structure M if there is a formula φ(x), expressible in the language of the structure, such that M ⊨ φ[a], while M ⊨ ¬φ[b] for all other objects b. We thus refer determinately to such a definable object a by mentioning this defining property φ, distinguishing this object from all the others. The structure is pointwise definable if indeed every individual is definable—every individual has a property that only it has.
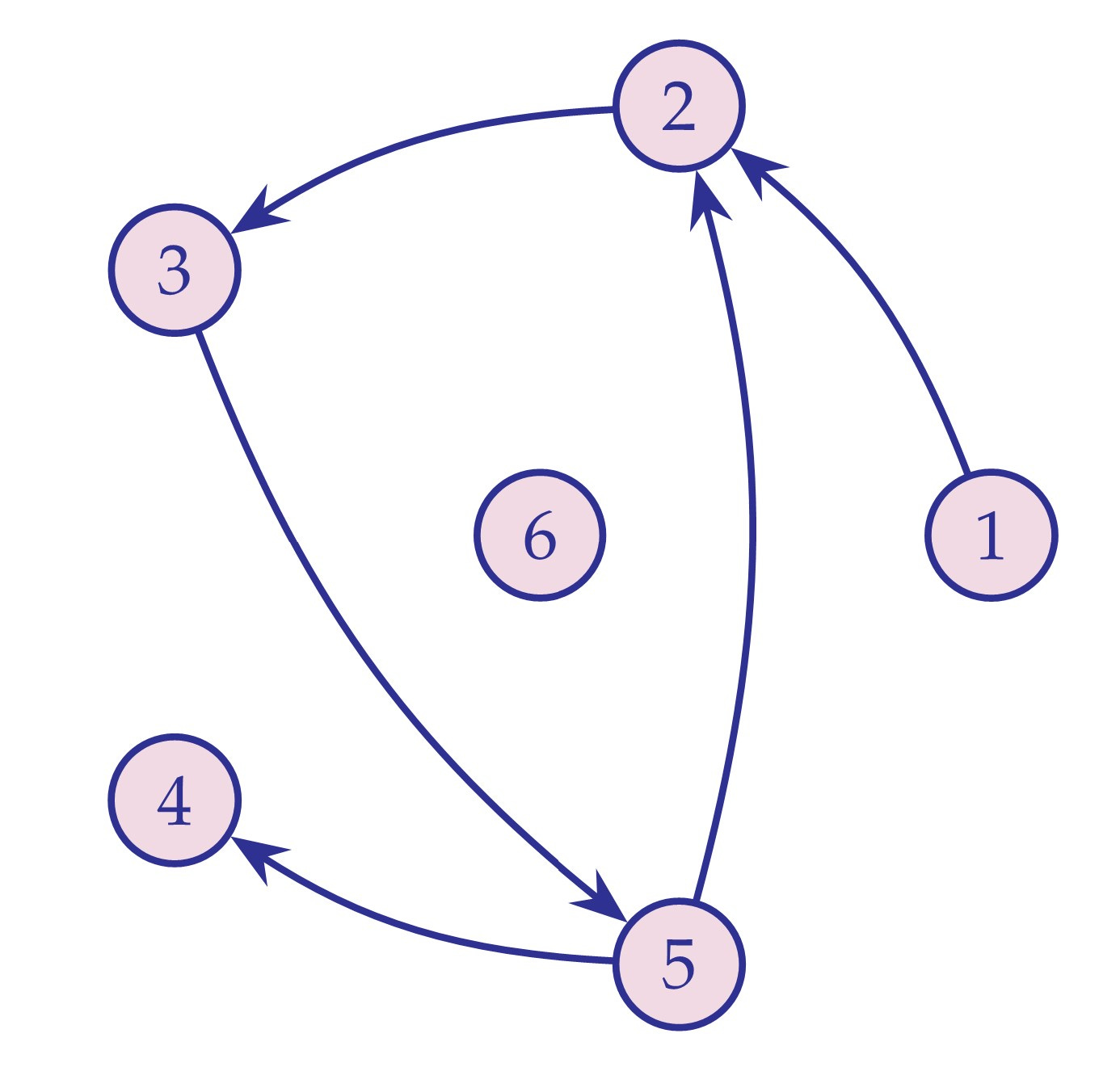
Consider the directed-graph structure shown here—there are six individuals in the domain and the language consists of the binary pointing-at relation Pab, indicated by the arrows.
Node 1 at the right has the property that it points at another node, but is not pointed at itself by any node. This is a defining property of node 1 in this structure, because only node 1 has this combination of features. And the property is expressible in the language of pointing-at, namely, node 1 is the only node x for which (∃y Pxy) ∧ ¬(∃y Pyx).
Thus, node 1 is definable in this structure. Node 4 is similarly definable, since it is the only node that is pointed at, but does not itself point at any node. Node 6 is the only node that neither points at nor is pointed at by any node. In fact, each of the nodes in this structure is definable in terms of the points-at relation. Can you find defining properties for the other nodes? Think about it before continuing.
Keep reading with a 7-day free trial
Subscribe to Infinitely More to keep reading this post and get 7 days of free access to the full post archives.