Skolem's paradox
Our best mathematical accounts of infinity exhibit a shocking lack of absoluteness—the very same set can be countable in one set-theoretic world, uncountable in another, and yet finite elsewhere.
This post is being made a little out of order—I received an inquiry recently about certain refined aspects of the topic, and so I am making the post available at this time. Although the essay makes references to ideas and results that I shall cover later in other posts, such as the Löwenheim-Skolem theorem and the compactness theorem, I believe nevertheless that for many readers the essay stands usefully now on its own terms. I hope you will enjoy it.
Skolem's paradox consists of an unsettling discovery at the very core of the foundations of mathematics, an observation concerning the necessarily indefinite nature of our conceptions of infinity. The fact of the matter is that all our best mathematical accounts of infinity exhibit an inherent, regrettable lack of absoluteness. It turns out, namely, that the question whether a given set is countable or uncountable, or even whether it is infinite at all, is not an inherent feature of the collection itself, but rather can depend on the set-theoretic background context in which the question is asked. Different models of set theory can have the very same set in common—they agree about which collection of objects the set is—and yet disagree about its size; they can disagree about whether the set is countably infinite or uncountably infinite or even whether it is infinite at all.
What? The same set can be finite in one set-theoretic world and uncountably infinite in another? Yes, alas, it is truly bonkers. Such is the unsettling nature of Skolem's paradox. Let me explain it.
The basic Skolem paradox—uncountable in a world, but actually countable
The most basic form of the paradox falls directly out of the downward Löwenheim-Skolem theorem, and so it is perhaps not surprising that it was Skolem who found it. One formulation of this theorem, which is by now a core result of model theory, states that for every first-order theory expressible in a countable language, if the theory has an infinite model, then it has a countably infinite model. A slightly stronger form of the theorem states that every infinite model in a countable language has a countable elementary substructure, that is, a countable submodel making exactly the same truth assertions about its objects as the parent model.
Allow me quickly to sketch the idea of the proof. If W is any model of the theory T, then we shall build a countable submodel M of it by starting with any countably many elements and then systematically adding witnesses—now called Skolem witnesses—for any existential statement
that is true in W about elements a we have already added to the submodel. By iteratively adding such witnesses x, we will form a countable submodel M ⊆ W that has witnesses for all such existential statements made in the parent model W about elements of the submodel M. It follows from this that truth in the submodel M aligns with truth in the parent model W about individuals in M, an observation that amounts to the Tarski-Vaught criterion. One simply proves by induction on formulas that the models agree: namely, atomic truth is the same in the submodel M as in the full model W; the two models agree on the truth calculations of Boolean operations; existential statements true in the submodel M will also be true in the parent model W, since inductively the same witnesses will work; and conversely, any existential statement true in the parent model W will find a witness in the submodel M precisely because of the Skolem witnesses. So the submodel M will thus agree on the truth of every assertion with the original model W—it is an elementary submodel M ≺ W. In particular, M is a countable model of the given theory T, as desired.
Since the language of set theory has just the one binary relation, the set-membership relation x ∈ y, we may apply the Löwenheim-Skolem theorem to conclude that if there is any model of Zermelo-Frankel ZFC set theory at all, then there is a countable model.
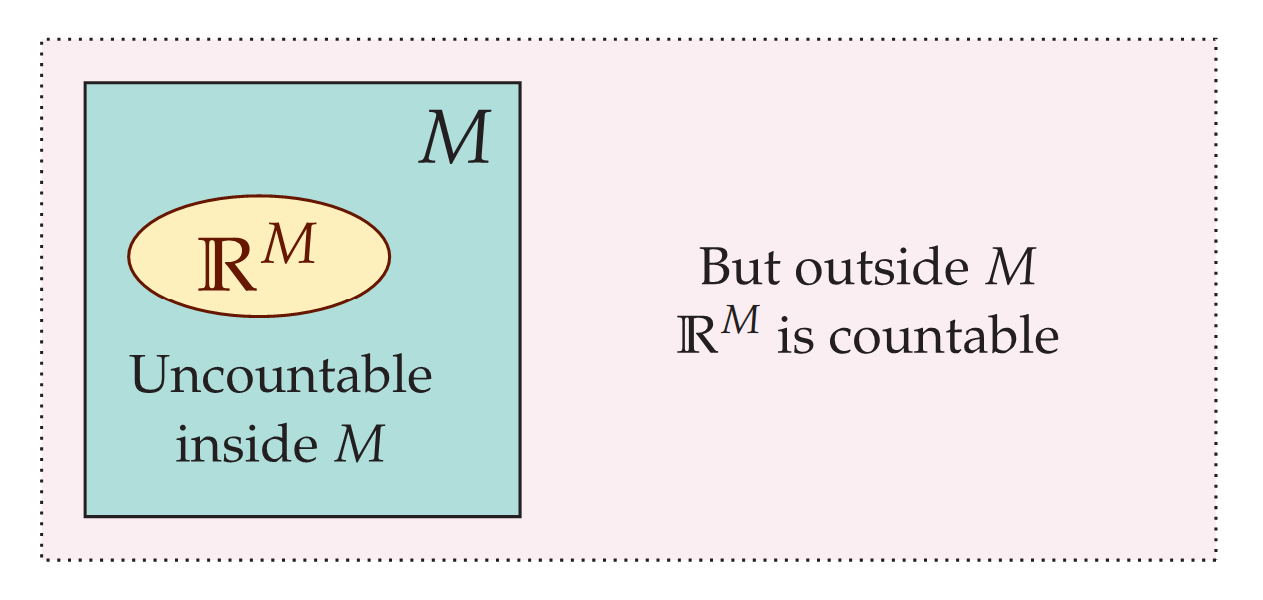
Consider now if you will the nature of set theory in a countable model M of ZFC. The theory ZFC proves, of course, that there exist many uncountable sets, such as the set of real numbers ℝ, Cantor space 2ω, the higher levels of infinity בω+5, and so forth. The theory ZFC proves that there is an abundance of such uncountable sets, and so M will have many such sets that it thinks are uncountable.
Paradox arrives, of course, with the observation that because M itself is countable, it offers only countably many objects altogether to constitute the elements of those supposedly uncountable sets. For instance, the model M has what it thinks is the set of real numbers—we might denote it by ℝM with a superscript to hightlight that this is M's version of the real numbers—and while M thinks that ℝM is an uncountable set, nevertheless we can see from outside M that this set has only countably many elements, appearing amongst the countably many individuals of M.
There are only countably many real numbers in M, countably many functions, countably many ordinals, countably many topological spaces, and so forth. In short, although M is its own set-theoretic ZFC universe, which looks upon many of its sets as uncountable, nevertheless, every set seen as uncountable in M is actually countable. How can a model of set theory be so wrong about uncountability?
Perhaps one begins to dissolve the paradox by contemplating exactly what it means for a model of set theory M to think that a set is countable or uncountable. A set is countably infinite in set theory if and only if there is a bijection of the set with a set of natural numbers. So a set x in M is thought to be uncountable from the perspective of M if it happens that there is no such bijection in M between the elements of x and a set of natural numbers as M sees them. This can be true even if, as with the countable model M above, there is such a bijection available outside the model. The model M just doesn't happen to have such a bijection, and this is why it views ℝM as uncountable, even though this is not actually true outside M.
Countable in a world, but actually uncountable
That was one kind of failure of absoluteness, where a set is seen as uncountable inside a model of set theory, but countable outside. Let us now describe the converse situation, where a set is countable inside a model of set theory, but uncountable outside. The question whether a set is countable or uncountable, therefore, fails absoluteness in both directions—countability is neither upwards absolute nor downwards absolute between set-theoretic worlds.
For this, we shall use the compactness theorem of first-order logic to produce a suitable nonstandard model of set theory. Specifically, suppose that the usual Zermelo-Frankel ZFC set theory is consistent, and let us expand the language with uncountably many new constant symbols ci for i ∈ I, where I is an uncountable set. Consider the theory ZFC together with the assertions “ci is a natural number” for every i in I—we may interpret natural numbers in set theory as usual via the finite ordinals—and also the axioms ci ≠ cj whenever i, j are distinct members of I.
Huh? How could there be so many different natural numbers? Surely this expanded theory is simply inconsistent? No, actually, this expanded theory is fully consistent, if ZFC itself is consistent. The reason is that every finite fragment of it can be interpreted inside any given model of ZFC. A finite fragment of the expanded theory, after all, will mention only finitely many of the new constant symbols, and these can therefore be interpreted amongst the ordinary natural numbers of the model. Since every finite fragment of the theory is thus consistent, it follows by the compactness theorem that the whole theory must also be consistent. Thus, the expanded theory is true in some model W.
The model W is a model of ZFC set theory with lots and lots of natural numbers, as viewed from outside W, since each ci is a distinct natural number in W for every i ∈ I. The natural numbers ℕW as W sees them are thus nonstandard, containing many more natural numbers than we have in our metatheoretic context. And yet, inside W this set is seen as countable—the set ℕW, after all, is viewed inside W as the canonical countably infinite set, the set of natural numbers. In particular, the model W does not know that it has a nonstandard ℕ and it will think all the usual arithmetic facts are true—every arithmetic assertion provable in ZFC will be true in ℕW.
In summary, what we have exhibited is a set-theoretic world W with a set ℕW that is thought to be countable in that world, but is seen as actually uncountable outside that world.
There is also an alternative construction of this phenomenon making use of ultrapowers. Namely, for any model of set theory M we can form inside M the internal ultrapower of the universe W = Mℕ / μ for some nonprincipal ultrafilter μ on ℕM in M. The model W is a model of ZFC that is a definable class in M—it is interpretable inside M from parameter μ. Some simple combinatorics arguments show that from the point of view of M, there are continuum many distinct natural numbers in W. So this is a case where we have two models of set theory, W visible inside M, with a set ℕW that is seen as countable inside W but uncountable inside M.
Finite in a world, but actually uncountably infinite
I should like to press the previous example rather much harder in order to achieve a more extreme or perhaps even shocking level of nonabsoluteness. Namely, what I claim is that the question whether a given set is finite or infinite also can depend on the set-theoretic world in which it is asked. We can find a model of set theory W with a set that is thought to be finite inside W, even while outside W we look upon the set as uncountably infinite!
This can be achieved by very similar means to our previous construction via the compactness theorem, if we should simply organize our theory a little more carefully. Namely, consider the theory augmenting ZFC with all the assertions that constants ci are distinct natural numbers, for i in some uncountable set I, plus one more constant c, asserting that it also is a natural number and ci < c for every i ∈ I. This theory is finitely consistent just as before, since any finite fragment of the theory mentions only finitely many constants, and these can be interpreted inside any fixed model of ZFC. So by the compactness theorem, the whole augmented theory is consistent.
Let W be a model of this newly augmented theory, and let us consider the nature of set theory that W provides. The model W again has its own set of natural numbers ℕW, which include its interpretations for all the constants ci and also the new constant c. Inside W, this object c is seen as a natural number. If x is the set of natural numbers below c in W, then W looks upon x as a finite set. Indeed, this would be the canonical finite set of size c in W, the set of numbers up to the given finite number c. So x is a finite set in W.
But outside W, we can see that x has as members all the distinct interpretations of the constants ci, an uncountable collection. So outside W we look upon x as an uncountable set. In short, we have a set-theoretic world W with a set x that W sees as finite, but which is actually uncountably infinite. Finiteness is consequently not upwards absolute between models of set theory.
This situation is also achieved by the ultrapower method, since the predecessors of any nonstandard natural number in the ultrapower by a nonprincipal ultrafilter on ℕ will have size continuum.
Positive instances of absoluteness
Despite the abundant instances of nonabsoluteness, there are nevertheless situations where positive absoluteness results are possible. First, we may observe that finiteness is always downwards absolute between set-theoretic worlds. If we are looking from a metatheoretic context down to a model of ZFC set theory M with a set x that we think in the metatheory has only finitely many elements, then indeed M will agree that it is finite. This can be seen by simple metatheoretic induction. Namely, the sets that are finite in M include the empty set and are closed under the addition of one element, and so by metatheoretic induction every set of M that is finite in the metatheory is finite in M. Equivalently, there cannot be set of smallest finite size in the metatheory but infinite in M, since removing an element would make a smaller set, therefore finite in M, but adding the element back in would therefore still be finite in M. These metatheoretic induction arguments show that every set in M that is finite in the metatheory will be finite in M.
This phenomenon underlies the similar observation that the metatheoretic natural numbers will always form an initial segment of the natural numbers of any model M that is available in that metatheoretic context. We can build an embedding n ↦ nM recursively in the meta theory, by mapping the metatheoretic zero 0 ↦ 0M to the zero of M, and for successors we map the metatheoretic successor to the successor as computed inside M:
This shows that the metatheoretic natural numbers are always included in the object theory natural numbers, which are standard when this is all of them and nonstandard when the model has additional natural numbers beyond them all.
Another positive instance of absoluteness is that the countability of a set x is always upward absolute from a model M whose natural numbers are standard. That is, if a set x is thought to be countable inside a model M and the natural numbers ℕM of the model are the standard natural numbers ℕ, then outside M we will also look upon x as countable. The reason is that the bijection that M has between the elements of x and a subset of the natural numbers will also serve as a suitable bijection for us, and so we will agree that x is countable.
This observation explains why it was a necessary feature of our previous counterexample to upward absoluteness of countability that the smaller world had a nonstandard ℕ. We had a model W with a nonstandard arithmetic ℕW, which was actually uncountable as seen from outside, even though inside W this set was seen as countable.
Forcing
We saw above with the Löwenheim-Skolem theorem how a set can be uncountable inside a set-theoretic model M, yet countable outside M. But I should like to mention another method of establishing this phenomenon, using the method of forcing, which achieves a far more robust effect. Forcing is a model-construction technique discovered by Paul Cohen in 1963, first used to establish the logical independence of the continuum hypothesis and the axiom of choice from the other axioms of set theory. Since that time set theorists have used forcing to prove thousands of similar independence results, and the forcing method has become a key set-theoretic tool. We have gained a deep understanding of the nature of set theory by using forcing to explore the diverse alternative set-theoretic worlds, realizing specific set-theoretic features. To my way of thinking, the discovery of this vast range of set-theoretic possibility has been the central discovery of set-theoretic research over the past half century.
The basic forcing method describes how to construct an extension model M[G] over a given set-theoretic universe M by adjoining a certain kind of ideal object G, a generic filter over a partial order ℙ in M. The forcing extension model M[G] is generated from the ground model M and the new object G, much like a field extension ℚ[√2] is generated from the base field ℚ and the new algebraic object √2 being adjoined to it. Every set in the forcing extension M[G] is the value of a name τ in the ground model M interpreted by the filter G.
The reason I mention forcing here is that this method provides much tighter examples of nonabsoluteness than we had above. One of the elementary facts about forcing is that it shows that any set at all can be made countable in a suitable forcing extension. Namely, if M ⊨ ZFC is a countable model of set theory and x is any set at all in M, then there is a forcing extension M[G] in which x is countable. But what makes this situation more robust is that the forcing extension M[G] has the same natural numbers and indeed the same ordinals as the original ground model M, and is otherwise very close to M. Forcing thus provides instances of nonabsoluteness for countability between models that are otherwise very close.
Pseudo-countability
A related concept is that of pseudo-countability. Namely, I define that a set or structure x is psuedo-countable if there is a set theoretic world W in which x, understood as the same collection of objects, is seen as countable. For example, we observed earlier that the natural number structure ℕW of a model of set theory W can be actually uncountable as seen from outside W, even when it is countable inside W. So this is an instance of psuedo-countability. In fact, for any model of set theory M, not necessarily countable, and any object x in M, there is an elementary extension M ≺ M* to a model M* over which there is a generic filter G such that x is countable in M*[G]. (If M is countable then we can take M = M*, and in this case x has the same elements in M as in M*[G], but otherwise it may gain new elements in M*.) This is a sense in which any structure at all can be seen as a countable structure in some world.
In my article “Pseudo countable models,” I explained how the pseudo-countability concept can be used to apply methods of countable structures to the uncountable. If we know a certain mathematical phenomenon applies to all countable structures of a certain type, and we have an uncountable structure x, then by moving to a set-theoretic world W in which x appears to be countable, we can apply the countable-structure result inside W. If the outcome of the result is sufficiently absolute, this allows us sometimes to extend methods from countable structures to the uncountable.
Iterative nonabsoluteness
Let me turn now to some more elaborate displays of nonabsoluteness, where the size judgement of a set flips and flops back and forth several times in succession in successively larger set-theoretic worlds. These examples show how truly wrong a model of set theory can be about the size of a set, even when it is subsequently thought wrongly to be right again, and then again thought wrongly to be wrong, and so on, wrong each time from the perspective of a still larger set-theoretic world, which is itself seen as wrong from a still larger context.
Finite-uncountable-countable
To illustrate the basic phenomenon I have in mind, let me provide three set-theoretic worlds M0 ⊆ M1 ⊆ M2 with a set x in the smallest world, with all three worlds agreeing on which collection of objects x is, except that x is seen as finite in M0, seen as uncountable in M1, and seen as countably infinite in M2.
For this, we can let M1 be any countable model of set theory. Let M0 be the internal ultrapower of M1 by a nonprincipal ultrafilter on ℕ. It follows that
is nonstandard as viewed from M1, and furthermore, every nonstandard natural number c in
will have continuum many predecessors as seen from M1. Let x be the predecessors of such a nonstandard natural number in M0. So M0 looks upon x as a finite set, but M1 thinks it has size continuum. Now let M2 = M1[G] be a forcing extension in which the continuum is collapsed to become countable. So M2 thinks x is a countably infinite set, as desired.
Finite-uncountable-countable-uncountable
Let us show next how to find such an example with a further model M3 inside of which x is seen as uncountable again.
We can simply let M3 be any countable model of set theory with a countable model of set theory M1* inside it, and let M1 be the internal ultrapower of M1* by a nonprincipal ultrafilter on ℕ. If we then build M0 and M2 relative to M1 as above, we will have a set x that is finite in M0, uncountable in M1, and countable in M2. But since M2 has the same natural numbers of M1, which arose as an ultrapower of M1* in M3, the model M3 looks upon x as uncountable.
Arbitrary iterations, finite-uncountable-countable-uncountable-countable-and-so-on.
We can continue in the same way to realize any finite pattern beginning with finite and then alternating between uncountably infinite and countably infinite. We shall have a sequence of models
with a set x that has all the same members in any of the models and which is finite in M0, uncountable in M1, countable in M2, uncountable in M3, countable in M4, uncountable in M5, and so forth, for any finite length.
These will all be realized in countable models of set theory. If the pattern ends with “uncountable” we can make it countable in a larger model by forcing. If the pattern ends with “countable”, then we can undertake the previous pattern inside the model arising as an ultrapower, meaning that the countably infinite set will be actually uncountable in the larger ambient world in which the previous pattern was realized. In this way, any finite pattern can be extended one more. Indeed, it is possible to build an infinitely iterated sequence of models realizing an infinitely long flip-flop pattern of countability and uncountability.
Note that we cannot reinsert “finite” into the pattern, because finiteness is always downward absolute. And whenever a countably infinite set is seen as uncountable in a larger world, it must be that the natural numbers of the smaller world are seen as nonstandard in the larger world.
The argument I have given here makes a consistency assumption about having models of set theory inside other models of set theory, which may seem to have a consistency strength exceeding ZFC. But in fact one doesn't need any assumption beyond the consistency of ZFC. The reason is that in any model of ZFC, it follows by the reflection theorem that every standard finite fragment of ZFC is true in some rank-initial segment of the universe Vα. And so if we start with a nonstandard model M, one having a nonstandard ℕ, then there will be some nonstandard fragment of ZFC that has a model in M, and this model will be an actual model of ZFC inside M, even if M sees it as satisfying only part of ZFC. Nevertheless, this is enough to carry out the iterated patterns in the construction I have described.
Bibliography
Joel David Hamkins, “Pseudo countable models,” Mathematics arXiv, October 2022, p. 1-11, arxiv:2210.04838.








I'm trying to write about Löwenheim-Skolem, just to mention it briefly for now (mostly through analogy). This post is great, I want to include a link for people that want more info if you don't mind!
Thank you for this wonderful article!
Zermelo–Fraenkel set theory, combined with first-order logic, aimed to give a precise account about the nature of infinite collections, with the ultimate goal to settle all controversial questions originating from "naive" set theory.
About a century later, we find that models of this theory are malleable like clay. We are looking at those models from an outside perspective, where we have confidence if some specific set is "genuine finite", "genuine countable", or "genuine uncountable", and have a lot of fun constructing models that would disagree from the inside perspective.
But how can we justify our confidence? For a finite set, I can look at some explicit syntactical representation, e.g, {{},{{}}}, which is clearly finite. I am unable to do the same for some infinite set, yet it seems easy to think about some very specific countable infinite set, e.g. the set X of all finite Von-Neumann ordinals, and convince myself that X is indeed equinumerous to the "genuine natural numbers". I can futher convince myself that the set Y of all subsets of X is uncountable.
We can do all this using our naive intuitive, semantic notion of a set is, outside of any formal theory, just like Cantor did. But of course, nothing prevents us from formalizing these statements in first order logic, and derive a purely syntactical a proof from the ZF axioms. Thus, by completeness, all models (including the most lunatic ones) will agree on the fact that X is indeed countable, and Y is indeed uncountable.
There is no paradox here, since from my outside perspective, I see that each model will point at different "genuine sets" X' and Y', claiming that these sets would be exactly those that I refer to as X and Y in my proof.
Now here is the catch: We may think we have pretty good understanding what the "real" sets X,Y look like. But do we? I for my part have some mental model of X and Y in my mind, but I am unable write down an explict representation (as in using nested braces like for a finite set) to show it to you. Instead, the best I can do is to try and give a precise definition. Likely, the most precise way to do this would be using some formal notions from set theory. And here we are back to square one.
This poses a philosophical problem: Is there such a thing as the "real X,Y" ? Is there even such a thing as a "genuine countable" set?
The platonist answer would be, that there is indeed, and anything else is just the weakness of first order logic. This was pretty much my own view when I first heard about Skolem's paradox. Today, I am not so sure anymore. Maybe it is more appropriate to think of "countability" as some structural concept that entails specific consequences, and just dismiss our outsider perspective at all? In the end, what prevents me from replacing the term "as seen from my outside perspective" by "as seen from a sufficiently strong formal model"? But this would be pure denial of the fact that I am able to reason about these sets in a rather informal way.