Structuralism
For mathematical insight, according to the structuralist imperative, investigate mathematical structure and consider mathematical concepts only as invariant under isomorphism.
Please enjoy this free extended excerpt from Lectures on the Philosophy of Mathematics, published with MIT Press 2021, an introduction to the philosophy of mathematics with an approach grounded in mathematics, arising organically from mathematical inquiry and practice. This book was used as the basis of my lecture series on the philosophy of mathematics at Oxford University.
Structuralism
Now that we have established Dedekind's categoricity result for arithmetic, let us discuss the philosophical position known as structuralism, in one form perhaps the most widely held philosophical position amongst mathematicians today. Contemporary structuralist ideas in mathematics tend to find their roots in Dedekind's categoricity result and the other classical categoricity results characterizing the central structures of mathematics, placing enormous importance on the role of isomorphism-invariance in mathematics. Much of the philosophical treatment of structuralism, meanwhile, grows instead out of Benacerraf's influential papers (1965, 1973).
The main idea of structuralism is that it just does not matter what numbers or other mathematical objects are, taken as individuals; what matters is the structures they inhabit, taken as a whole. Numbers each play their structural roles within a number system, and other mathematical objects play structural roles in their systems. The slogan of structuralism, according to Shapiro (1996, 1997), is that “mathematics is the science of structure.”
A defining structural role played by the number zero in any copy of the ring of integers ℤ is that it is the additive identity. It also happens to be the unique additive idempotent, the only number z for which z + z = z; it is the only additively self-inverse number z = -z; and it is the smaller of the two multiplicative idempotents. So in general, there can be many ways to characterize the role played by a mathematical object. In the rational numbers ℚ, the number 1/2 is the only number whose sum with itself is the multiplicative identity 1/2 + 1/2 = 1. In the real field ℝ, the defining structural role played by √2 is that it is positive and its square is equal to 2, which is 1 + 1, where 1 is the multiplicative identity.
Yet, one should not confuse structural roles with definability. Tarski's theorem on real-closed fields, after all, implies that the number π, being transcendental, is not definable in the real field ℝ by any property expressible in the language of ordered fields. Yet it still plays a unique structural role, determined, for example, by how it cuts the rational numbers into those below and those above; only it makes exactly that same cut.
Definability versus Leibnizian structure
Let me elaborate. An object a in a structure M is definable in that structure if it has a property φ(a) in M that it alone has — a property expressible in terms of the structural relations of M, which picks out this object a uniquely. This is relevant for structuralism, because the definition φ specifies explicitly the structural role played by the object in that structure. A structure is pointwise definable if every object in it is definable in this way.
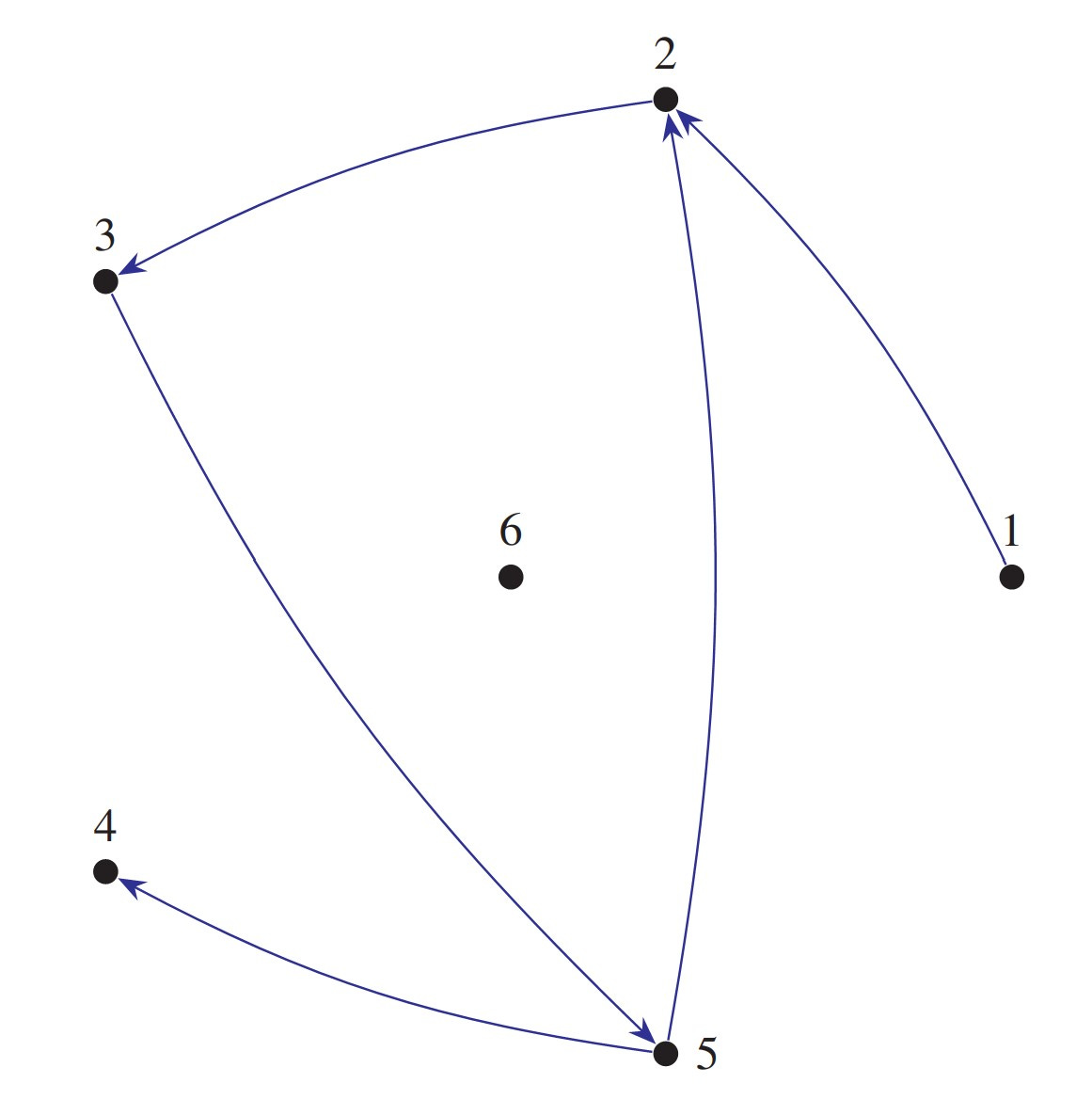
In the directed graph pictured here, for example, node 2 is the unique node that is pointed at by a node that is not pointed at by any node (namely, 2 is pointed at by 1, which is not pointed at at all); and node 4 is the unique node that is pointed at by a node, yet does not itself point at any node. In fact, every node in this graph is characterized by a property expressible in terms of the pointing-at relation, so this graph is pointwise definable. A mathematical structure is Leibnizian, in contrast, if any two distinct objects in the structure can be distinguished by some property. In other words, a Leibnizian structure is one that fulfills Leibniz's principle on the identity of indiscernibles with respect to properties expressible in the language of that structure.
Every pointwise definable structure is Leibnizian, since the defining properties of two different objects will distinguish them. But the notions are distinct. For example, the real ordered field ⟨ℝ, + , · ,<,0,1⟩ is Leibnizian, since for any two distinct real numbers x < y, there is a rational number p/q between them, and x has the property that x < p/q, while y does not, and this property is expressible in the language of ordered fields. But this structure is not pointwise definable because there are only countably many possible definitions to use in this structure, but uncountably many real numbers, so they cannot all be definable.
Every Leibnizian structure must be rigid, meaning that it admits no nontrivial automorphism, because automorphisms are truth-preserving — any statement true of an individual in a structure will also be true of its image under any automorphism of the structure. If all individuals are discernible, therefore, then no individual can be moved to another. Because of this, we should look upon the Leibnizian property as a strong form of rigidity. These two concepts are not identical, however, because there can be rigid structures that are not Leibnizian. Every well-order structure, for example, is necessarily rigid, but when an order is sufficiently large — larger than the continuum is enough — then not every point can be characterized by its properties, simply because there aren't enough sets of formulas in the language to distinguish all the points, and so it will not be Leibnizian. Indeed, for any language ℒ, every sufficiently large ℒ-structure will fail to be Leibnizian for the same reason.
The rigid relation principle, introduced and investigated by Hamkins and Palumbo (2012), is the mathematical principle asserting that every set carries a rigid binary relation. This is a consequence of the well-order principle, because well-orders are rigid, but it turns out to be strictly weaker; it is an intermediate weak form of the axiom of choice, neither equivalent to the axiom of choice nor provable in ZF set theory without the axiom of choice.
Role of identity in the formal language
The nature of Leibnizian structures is often sensitive to the question of whether one has included the equality or identity relation x = y in the formal language. In contemporary approaches to model theory and first-order logic, it often goes without saying that equality is included as a logical relation in every language and interpreted in every model as actual equality. This is ultimately a convention, of course, and one can easily and sensibly undertake a version of model theory without treating equality in this special manner.
When one omits equality from the language, then every model is elementarily equivalent to a model that violates the Leibnizian principle on the identity of indiscernibles. Specifically, for any model M in a language without equality, consider a new model M* obtained by adding any number of duplicate elements for any or all of the elements of M, defining the atomic relations for the duplicates in the new structure M* in accordance with the original structure. For example, in the rational order ⟨ℚ, ⩽ ⟩, we might consider the order ⟨ℚ*, ⩽ ⟩ in which every rational number has two copies, each less-than-or-equal to the other and ordered with the other elements as one would expect, so that both copies of 0, for example, are less than any of the copies of positive elements, and so on. It follows inductively that any equality-free statement φ(a0,...,an) true of individuals in M will also be true in M* of any of their duplicates φ(a0*,...,an*). In particular, the structure M* will not be able to discern an individual from its copies, and so this structure will not be Leibnizian if indeed any nontrivial duplication occurred. Furthermore, the two models have exactly the same equality-free truth assertions; they are elementarily equivalent in that language. (Meanwhile, with equality we can distinguish the models, since ⩽ is anti-symmetric in ℚ, meaning that
but this is not true in ℚ*.)
The philosophical point to make about this is that one can never expect a theory to give rise to the Leibnizian principle of identity of indiscernibles, unless the language includes the equality relation explicitly. In particular, nothing you say about a nonempty structure can possibly ensure that it is Leibnizian, unless equality is explicitly mentioned, since the structure has all the same equality-free assertions as the corresponding structure in which every individual has been duplicated.
Isomorphism orbit
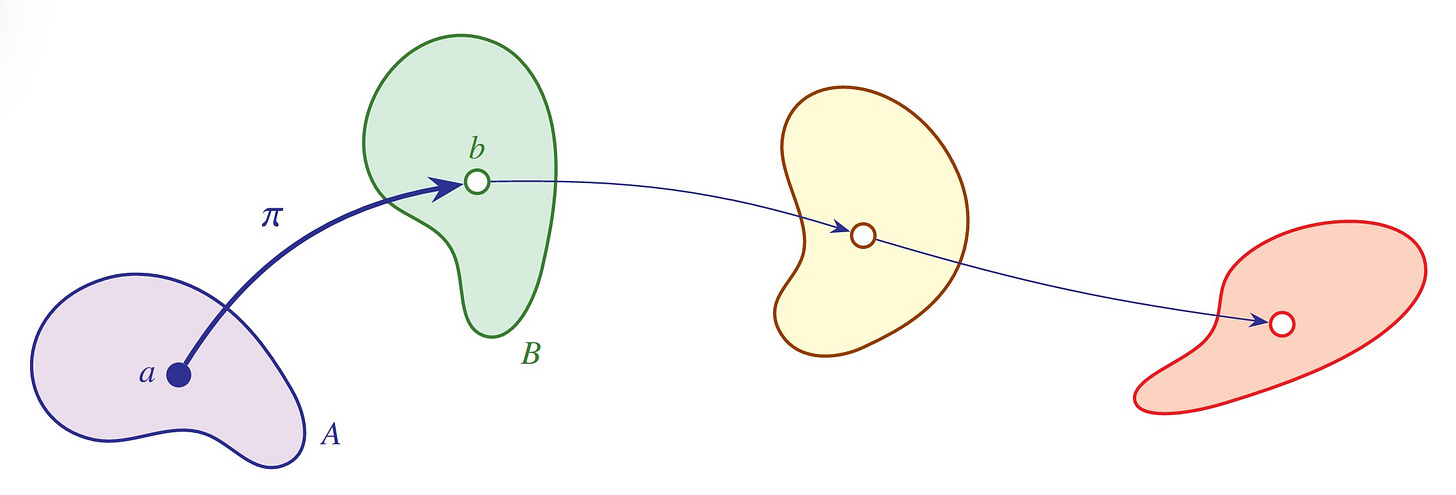
While definability and even discernibility are sufficient for capturing the structural roles played by an object, they are not necessary, and a fuller account will arise from the notion of an isomorphism orbit. Specifically, two mathematical structures A and B are isomorphic if they are copies of one another, or more precisely, if there is an isomorphism π:A → B between them, a one-to-one correspondence or bijective map between the respective domains of the structures that respects the salient structural relations and operations. For example, an order isomorphism of linear orders ⟨L1, ⩽1⟩ and ⟨L2, ⩽2⟩ is a bijection π:L1 → L2 between the domains of the orders that preserves the order structure from one to the other, meaning that x ⩽1 y if and only if π(x) ⩽2 π(y). An isomorphism of arithmetic structures ⟨Y,+,·⟩ and ⟨Z,⊕,⊗⟩ is a bijection τ:Y → Z, for which τ(a + b) = τ(a) ⊕ τ(b) and τ(a · b) = τ(a) ⊙ τ(b), translating the structure from Y to Z. Every mathematical structural conception is accompanied by a corresponding isomorphism concept.
The isomorphism concept is intricately linked with that of formal language, which is a way of making precise exactly which mathematical structure one is considering. Whether a given one-to-one correspondence is an isomorphism depends crucially, after all, on which structural features are deemed salient. Is one considering the rational numbers only as an order, or as an ordered field? A given bijection may preserve only part of the structure.
Structural roles are respected by isomorphism, and indeed, they are exactly what is respected by isomorphism. An object a in structure A plays the same structural role as object b in structure B exactly when there is an isomorphism of A with B carrying a to b.
So let us consider the isomorphism orbit of an object in a structure, the equivalence class of the object/structure pair (a,A) with respect to the same-structural-role-as relation.
This orbit tracks how a is copied to all its various isomorphic images in all the various structures isomorphic to A. And whether or not these objects are definable or discernible in their structures, it is precisely the objects appearing in the isomorphism orbit that play the same structural role in those structures that a plays in A.
Categoricity
A theory is categorical if all models of it are isomorphic. In such a case, the theory completely captures the structural essence of what it is trying to describe, characterizing that structure up to isomorphism. Dedekind, for example, had isolated fundamental principles of arithmetic and proved that they characterized the natural numbers up to isomorphism; any two models are isomorphic. In other words, he proved that his theory is categorical.
The analogous feat has long been performed for essentially all the familiar mathematical structures, and we have categorical characterizations not only of the natural numbers ℕ, but of the ring of integers ℤ, the field of rational numbers ℚ, the field of real numbers ℝ, the field of complex numbers ℂ, and many more (see sections 1.11 and 1.13). Daniel Isaacson (2011) emphasizes the role that categoricity plays in identifying particular mathematical structures. Namely, we become familiar with a structure; we find the essential features of that structure; and then we prove that those features axiomatically characterize the structure up to isomorphism. For Isaacson, this is what it means to identify a particular mathematical structure, such as the natural numbers, the integers, the real numbers, or indeed, even the set- theoretic universe.
Categoricity is central to structuralism because it shows that the essence of our familiar mathematical domains, including ℕ, ℤ, ℚ, ℝ, ℂ, and so on, are determined by structural features that we can identify and express. Indeed, how else could we ever pick out a definite mathematical structure, except by identifying a categorical theory that is true in it? Because of categoricity, we need not set up a standard canonical copy of the natural numbers, like the iron rod kept in Paris that defined the standard meter; rather, we can investigate independently whether any given structure exhibits the right structural features by investigating whether it fulfills the categorical characterization.
Invariably, for deep reasons, these categorical characterizations use second-order logic, meaning that their fundamental axioms involve quantification not only over the individuals of the domain, but also over arbitrary sets of individuals or relations on the domain. Dedekind's arithmetic, for example, asserts the induction axiom for arbitrary sets of natural numbers, and we shall see in section 1.11 that Dedekind's completeness axiom for the real numbers involves quantifying over arbitrary bounded sets of rational numbers.
The deep reasons are that a purely first-order theory, one whose axioms involve quantification only over the domain of individuals in a structure rather than over arbitrary sets of individuals, can never provide a categorical characterization of an infinite structure. This is a consequence of the Löwenheim-Skolem theorem, which shows that every first-order theory that is true in an infinite model is also true in models of diverse infinite cardinalities, which therefore cannot be isomorphic. Meanwhile, the Löwenheim-Skolem theorem does not apply to second-order theories, and it should be no surprise to find second-order axioms in the categorical theories characterizing our familiar mathematical structures.
Some philosophers object that we cannot identify or secure the definiteness of our fundamental mathematical structures by means of second-order categoricity characterizations. Rather, we only do so relative to a set-theoretic background, and these backgrounds are not absolute. The proposal is that we know what we mean by the structure of the natural numbers—it is a definite structure—because Dedekind arithmetic characterizes this structure uniquely up to isomorphism. The objection is that Dedekind arithmetic relies fundamentally on the concept of arbitrary collections of numbers, a concept that is itself less secure and definite than the natural-number concept with which we are concerned. If we had doubts about the definiteness of the natural numbers, how can we assuaged by an argument relying on the comparatively indefinite concept of “arbitrary collection”? Which collections are there? The categoricity argument takes place in a set-theoretic realm, whose own definite nature would need to be established in order to use it to establish definiteness for the natural numbers.
Structuralism in mathematical practice
I should like to contrast several forms of structuralism, distinguishing first a form of structuralism that is widespread amongst mathematicians—a form which I call structuralism in practice. Structuralism in practice involves an imperative about how to undertake mathematics, a view about which kinds of mathematical investigations will be fruitful. According to the structuralist-in-practice, mathematics is about mathematical structure, and mathematicians should state and prove only structuralist theorems in a structuralist manner. All of one's mathematical concepts should be invariant under isomorphisms.
The structuralist imperative. For mathematical insight, investigate mathematical structure, the relations among entities in a mathematical system, and consider mathematical concepts only as being invariant under isomorphism. Therefore, do not concern yourself with the substance of individual mathematical objects, for this is mathematically fruitless as structure arises with any kind of object.
According to the structuralist imperative, it would be mathematically misguided to state theorems about particular instantiations of mathematical structure; a theorem involving the real numbers, for example, should do so in a way that it becomes invariant under isomorphism; one should be able to replace the real numbers with any other complete ordered field, while preserving the truth of the theorem. The structuralist-in-practice dismisses questions about the “true nature” of mathematical objects—about what numbers “actually” are—as mathematically irrelevant.
It would accord with the structuralist imperative, for example, to prove a theorem about the countable random graph if one takes this term to refer to any countable graph with the finite pattern property, a feature that characterizes these graphs up to isomorphism. One might prove, for example, that the countable random graph is homogeneous or that it has diameter two or an infinite chromatic number; what this really means is that all such countable graphs with the finite pattern property have these features. Because the hypothesis is invariant under isomorphism, we do not care which particular copy of the countable random graph we are using, and this is the heart of structuralism.
It would be antistructuralist, in contrast, to state those theorems specifically only about the Rado graph if this is taken to refer to the specific graph relation on the natural numbers with an edge between n and m, where n < m, if the nth binary digit of m is 1; this graph happens to exhibit the finite pattern property, and therefore it is a specific instance of the countable random graph (once one has fixed a copy of the natural numbers).
Notice that it would be fine, logically, to prove something about the countable random graph by proving it specifically about the Rado graph, even using specific features of the Rado graph, provided that the theorem itself was invariant under graph isomorphisms, for then it would transfer from the Rado graph to all copies of the countable random graph. In this sense, it might seem that structuralism in practice requires only that one's theorems are structuralist, that is, that they are properly invariant under isomorphism.
Yet, the structuralist imperative recommends against that style of proof, against using nonstructural details of one's specific interpretation instances, even when they might seem convenient. The reason is that those details never lie at the core of the mathematical phenomenon—they are always a distraction—precisely because they cannot matter for the structuralist conclusion of the theorem. If you have a proof of an isomorphism-invariant theorem that uses incidental details of a specific instantiation, then the mathematical structuralist will say that you have a poor argument; you have missed the essential point; and your argument will not produce mathematical insight. In this sense, the structuralist imperative is a recommendation about mathematical efficacy. Namely, by undertaking structural arguments, we will stay closer on the trail of mathematical truth.
Meanwhile, it would be structuralist to prove theorems about the Rado graph if one was concerned with some of the extra structure inherent in that particular presentation of this graph. For example, the edge relation of the Rado graph is a computably decidable relation on the natural numbers, but not every copy of the countable random graph on the natural numbers is computably decidable. In this case, one is not really studying the countable random graph, with only its graph structure, but rather one is studying computable model theory, looking at the computational complexity of presentations of this graph. This is again structural, but with different additional structure beyond pure graph theory.
Consider a structuralist analogy with computer programming. A structuralist approach to programming treats its data objects only with respect to the structural features explicitly in the defining data types; this way of programming is often portable to other operating systems and implementations of the programming language. It would be antistructuralist for a program to use details of how a particular piece of data is represented on a particular system, to peek into the internal coding of data in the machine; this sneaky way of getting at the data might work fine at first, but it often causes portability issues because the methods can fail when one changes to a different machine, which might represent the data differently “under the hood,” so to speak.
The structuralist imperative tends to lead one away from the junk-theorem phenomenon, for junk is often particularly objected to, specifically because it is antistructuralist (but consider question 1.19 as a counterpoint). The structuralist-in-practice dismisses the Julius Caesar objection as misguided, for it does not matter what the cardinal numbers are, so long as they obey the Cantor-Hume principle, and so we do not care if any of them are Julius Caesar or not. Indeed, we can easily define an interpretation of number in which Julius Caesar is the number 17, or not, and everything in our theory will work fine either way. There is nothing mathematical at stake in it.
Some mathematicians have emphasized that in some of the category-theoretic foundations, such as in ETCS, the formal languages provided for these systems are necessarily invariant under isomorphisms. When working in those languages, therefore, one cannot help but follow the structuralist imperative.
Eliminative structuralism
What I am calling structuralism in practice is closely related to eliminative structuralism (also called post-rem structuralism), defended by Benacerraf (1965)—namely, the view that mathematical structure is simply that which is instantiated in particular structures. Eliminative structuralism includes the nominalist claim that there is no abstract object that is the mathematical structure itself, beyond representations in particular instantiations. There is no abstract thing that is “the number 3”—any object can play that role in a suitable structure—and so talk of numbers and other particular mathematical objects is merely instrumental. Shapiro (1996) says, “Accordingly, numerals are not genuine singular terms, but are disguised bound variables.” A reference to the number 3 really means: in the model of Dedekind arithmetic at hand, the successor of the successor of the successor of zero.
One difference between structuralism in practice and eliminative structuralism, however, is that the structuralist-in-practice drops the elimination claim, the nominalist ontological claim that abstract structural objects do not exist; rather, the structuralist-in-practice simply follows the structuralist imperative to pursue isomorphism-invariant mathematics, whether abstract structural objects exist or not. And since elimination is not part of the view, it would seem wrong to call it eliminative structuralism.
Another form of eliminative structuralism is the view of modal structuralism, also called in-re structuralism and defended by Geoffrey Hellman, according to which assertions about mathematical objects are to be understood modally as necessary claims about their possible instantiations. According to this view, mathematical structures are ontologically dependent on the systems that exemplify them. In extreme form, one might hope to reduce mathematical structure ultimately to concrete physical systems. And there is also a relative form of eliminative structuralism, which reduces structure to sets. Namely, according to set-theoretic reductionism, an extreme form of set-theoretic foundationalism, structure does not exist apart from its set-theoretic realizations, such as by means of the isomorphism orbit. This is different from merely using set theory as a foundation of mathematics, since one can propose set theory as a foundation simply by interpreting mathematical structure within set theory, without insisting that there is no structure outside of set theory.
Abstract structuralism
There is something a little puzzling about the structuralist mathematician, who follows the structuralist imperative, yet happily refers to the natural numbers and the number 17 and the real number π. If we only care about the natural numbers up to isomorphism, after all, then there is not any longer a unique mathematical object or structure corresponding to these terms, and so what is meant by “the” here? It would seem that the structuralist-in-practice should be referring instead to a natural numbers or a number 17. But mathematicians do not generally talk that way, even when they are structuralist. Structuralism seems to face a serious problem with singular reference.
To be sure, most mathematicians, when pressed about their singular references, articulate the structuralist-in-practice view. They say that it does not matter to them which copy of the natural numbers we use, and that by 17, they mean to refer to the object playing that role in whichever version we currently have. Thus, they have dutifully inserted Shapiro's disguised quantifiers.
But some philosophers aim for a more robust solution to the problem of singular reference. According to abstract structuralism, also known as ante-rem structuralism, defended by Stewart Shapiro (1997), Michael Resnik (1988), and others, the objects of mathematics, including numbers, functions, and sets, are inherently structural; they exist as purely structural abstract objects, positions within a structure, locations in a pattern of arrangement that might be realized in diverse instantiations. The quarterback is a position on an American football team, the role played by the person who calls the play, receives the hike and makes the passes. Each individual quarterback is a person rather than a position — a person who plays the role of quarterback on a particular team. Similarly, the natural number 3 is the third successor “location” in the natural number structure — the position that any particular copy of 3 fills in any particular instantiation of the natural numbers. On this view, mathematical structure exists independently of the particular systems instantiating that structure.
Abstract structuralism provides a direct account of the reference of singular terms in mathematics, explaining how the number 3 and the natural numbers can sensibly refer, even from a structuralist perspective, to the purely structural object or the abstract structural role played by these entities. One undertakes the Fregean process of abstraction from the same-structural-role relation, whose equivalence classes are precisely the isomorphism orbits. Every isomorphism orbit leads one by abstraction to a corresponding abstract structural role. Shapiro also argues, much like Maddy in the egg carton argument (mentioned on page 21), that abstract structuralism offers a solution to Benacerraf's epistemological problem: we gain access to finite instances of abstract structures and then proceed by abstraction to the structure itself.
The abstract structuralist is providing a structuralist account of mathematics by realizing mathematical objects as purely structural. Yet, the structuralist-in-practice will say that this form of abstract structuralism is not structuralist at all—it violates the structuralist imperative—precisely because it is concerned with what the mathematical objects are, even if the answer it provides is that they are purely structural. According to the structuralist-in-practice, such concerns are misguided; they never elucidate a mathematical phenomenon and are irrelevant for mathematical insight. The structuralist-in-practice will happily consider any classification invariant of the isomorphism orbit relation, such as the orbit itself (akin to Frege taking numbers as equinumerosity classes), without the need for a purely structural abstract object representing the structural role.
Yet, the abstract structuralist may reply, “Fine, we do not pursue abstract structuralism for mathematical insight, but rather as a philosophical investigation in mathematical ontology, aiming to understand what mathematical structure really is.” The abstract structuralist seeks to identify and elucidate the essential nature of mathematical objects, a philosophical effort rather than a mathematical one. The abstract structuralist seeks to give an account of what structure is—the thing that the mathematicians take to be so fundamental.
Jump into the middle of one of my Oxford lectures where I discuss this topic: (go to 33:20s for structuralism)




Great article! I find the discussion of the different strands of philosophical structuralism illuminative.
What, if any, implications those varieties of structuralism have on "The Unreasonable Effectiveness of Mathematics in the Natural Sciences"?