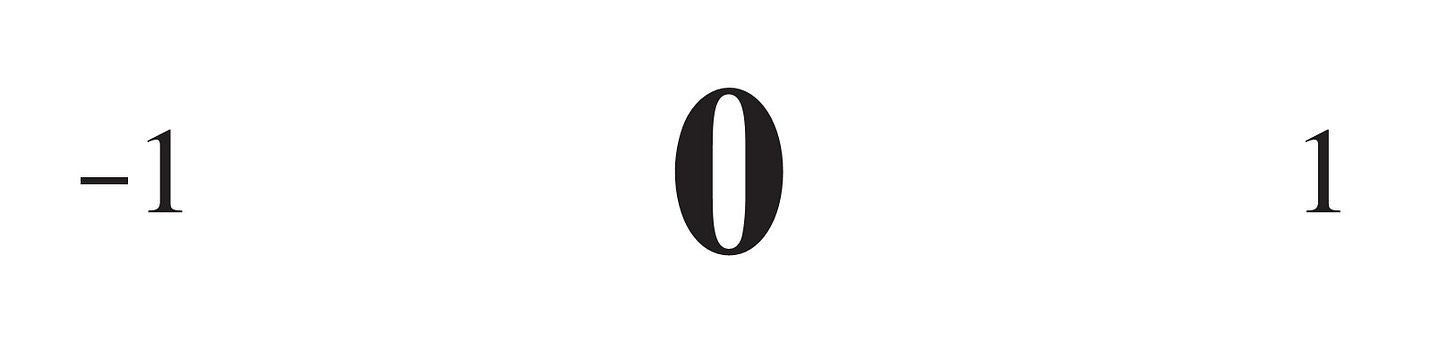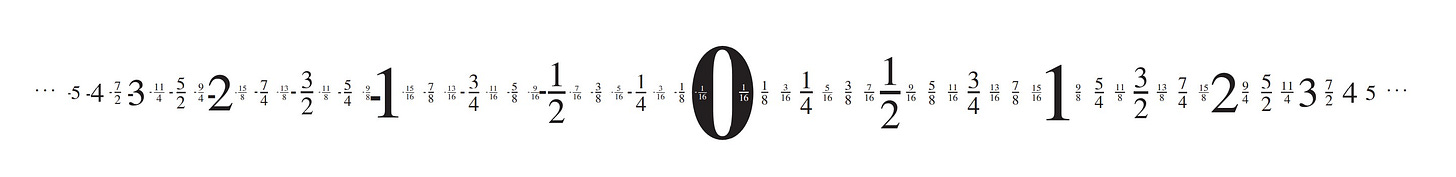The surreal numbers

All the numbers great and small. The surreal numbers, generated in a recursive process of completion, unify the real numbers, the ordinals, and the infinitesimals in a single stupendous number system.

Join me, friend! Let us endeavor together to build the numbers, ALL the numbers, great and small. We shall construct the surreal number system, that monumental ediface of numbers, encompassing all the most familiar numbers, to be sure—the natural numbers, the integers, the rational numbers, and the real numbers—but including also the transfinite ordinals, the infinitesimals, and all the strange new numbers that arise in combination from these, like √ω - π/ω², mixing together the infinitely large with the infinitely small. The surreal numbers unify all these number systems into one colossal yet systematically coherent and graceful new number system.

Surreal number generation

The surreal numbers grow from absolutely nothing to an awesome structure, generated by a single elegant rule—applied recursively, endlessly, transfinitely—a simple recursive instruction telling us how to create new surreal numbers from the previously created numbers and how to order the surreal numbers amongst each other. The entire surreal number system grows out of this simple process of completion.

Surreal number generation rule: Iteratively fill all gaps. At every stage, in all possible ways, separate the numbers constructed so far into a lower set and an upper set and create a new surreal number sitting strictly between them, filling this gap.

According to the generation rule, at every stage we divide the current numbers into a lower set L and an upper set R, meaning that every element of L is less than every element of R, and we create a new surreal number x sitting exactly between them, so that x_L < x for every x_L in the lower set and x < x_R for every x_R in the upper set. We can denote this newly created number using the surreal numeral notation

\(\newcommand{\set}[1]{\{\,{#1}\,\}} x = \set{L \mid R}. \)

The numeral specifies for this number x exactly the circumstances of its birth.

The surreal genesis, the big bang of numbers

But we have gotten ahead of ourselves. Let us investigate how the surreal number generation rule works from the very start. At the beginning, of course, we have created no numbers yet. How are we to divide this nothing into a lower set and an upper set? We simply take both the lower set and the upper set as empty, of course.

And then a truly remarkable event occurs, for according to the surreal number generation rule, applied even in this trivial instance, a new point is created having so far nothing previous below it and nothing previous above it, a newly created point filling this empty cut. Thus is born the first surreal number, the number zero, born on day 0. We have created something from nothing. We are witnessing the surreal genesis, the big bang of numbers.

The surreal numeral for zero is written with empty lower and upper sets, like this:

\( 0 = \set{\ \ | \ \ }. \)

Being the very first number, zero has no previously created numbers below it and no previously created numbers above it.

Having created this number 0, we are now able to specify further separations relative to it, of course, either by placing 0 into a new lower set or into a new upper set. Thus on day 1 we create the number one, the first-born number larger than zero,

\( 1 = \set{0\mid \ \ } \)

and also the number negative one, the first-born number less than zero,

\( -1 = \set{\ \ | \ 0}.\)

Thus altogether so far we have created three surreal numbers.

We proceed immediately to make four cuts in these numbers, thereby creating four new surreal numbers, born on day 2:

The number ½ arises specifically to occupy the gap between 0 and 1 and is therefore denoted ½ = { 0 | 1 }, but it is more fully specified as { -1 0 | 1 }. And the number -2 = { | -1 } is newly created as the first-born number below -1. Can you write down the numerals of the other numbers here?

On day 3 we form further separations of these numbers and create new numbers to fill all the resulting gaps that we are now able to specify relative to them.

The elegant surreal number line thus gradually emerges.

New numbers are created at each stage, which are then be used to form further separations and therefore still more numbers, a doubling of the points (plus one) at each finite stage.

The surreal numbers are accumulating around us. Let us investigate!