The orders of infinity

What is the spectrum of possible behavior at infinity for a real-valued function on the reals? What are the possible rates of growth? What is the structure and complexity of these orders of infinity?

Consider the various functions f : ℝ → ℝ on the real numbers and the vastly different behaviors they might exhibit as they progress to infinity. Some may tend to zero, others settle into a modest linear growth, and still others might grow superexponentially.

What is the range of possibility? For that matter what does it mean precisely—and what should it mean—to say that two functions exhibit the same behavior at infinity? What are the possible rates of growth? What is the structure and complexity of these “orders of infinity”?

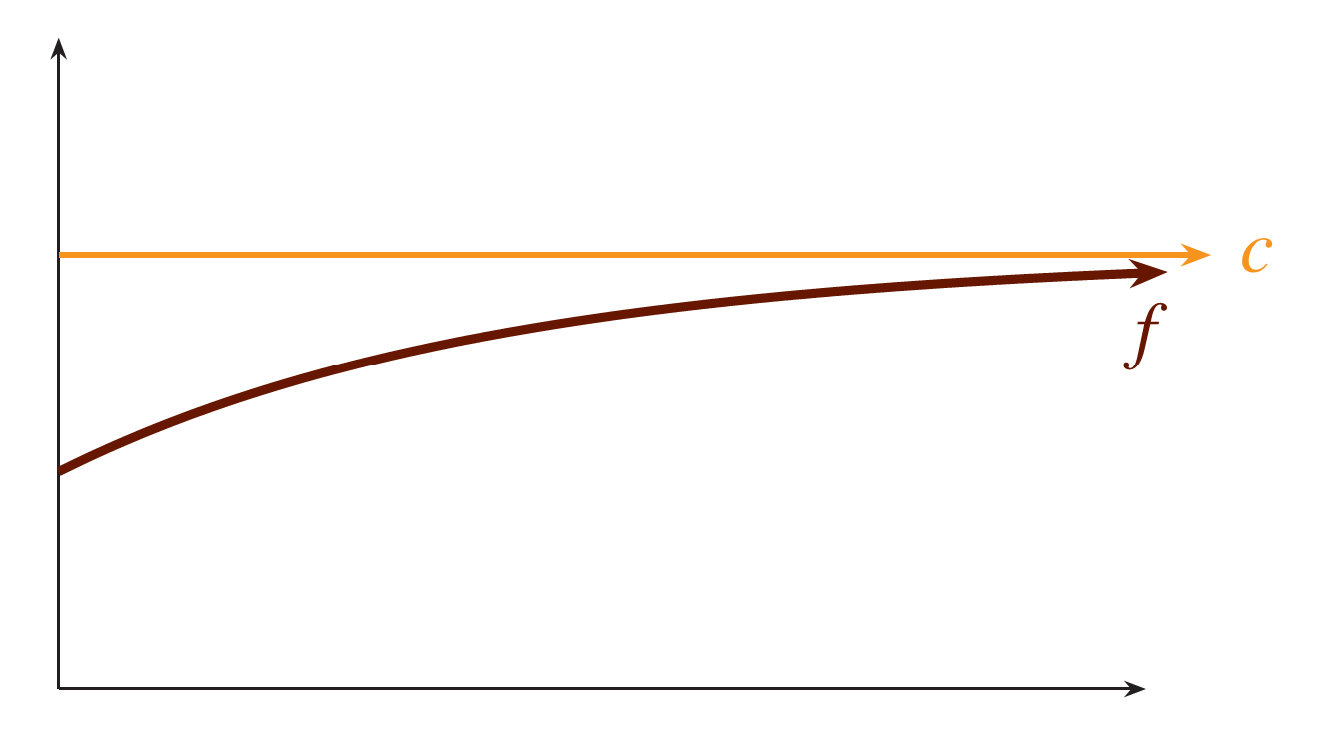
Consider a simple case—a constant function y = c. Perhaps a function f approaching it with a horizontal asymptote

\(\lim_{x → ∞ } f(x)=c\)

could be said to exhibit the same behavior “at infinity.”

A linear function could similarly be said to have the same behavior at infinity as a function with that line as a slant asymptote.

And so on with other functions. To understand the range of possibility, we would like somehow to group together functions that exhibit the same behavior at infinity.

But what does this mean exactly? We would like to be able to express the idea that two functions have the same limiting behavior. What is the precise criteria we are seeking?

The orders of infinity

What we seek is to define an equivalence relation that captures and expresses the intuitive notion of two functions having the same behavior at infinity. It turns out that there are a variety of natural ways to go about this, depending on whether one seeks a fine or coarse conception.