Throwing Darts at the Real Line

Mathematical philosophers have proposed various thought experiments suggesting different resolutions of the continuum hypothesis. Can we hope legitimately to answer the question this way?

Although we cannot expect to settle the continuum hypothesis based on proof from the standard ZFC axioms of set theory—it is independent of those axioms, after all, neither provable nor refutable—we might hope to settle it on other grounds. Several mathematical philosophers have proposed various philosophical thought experiments as a way to gain insight into what our attitude toward the continuum hypothesis should be or could have been.

Freiling's Axiom of Symmetry

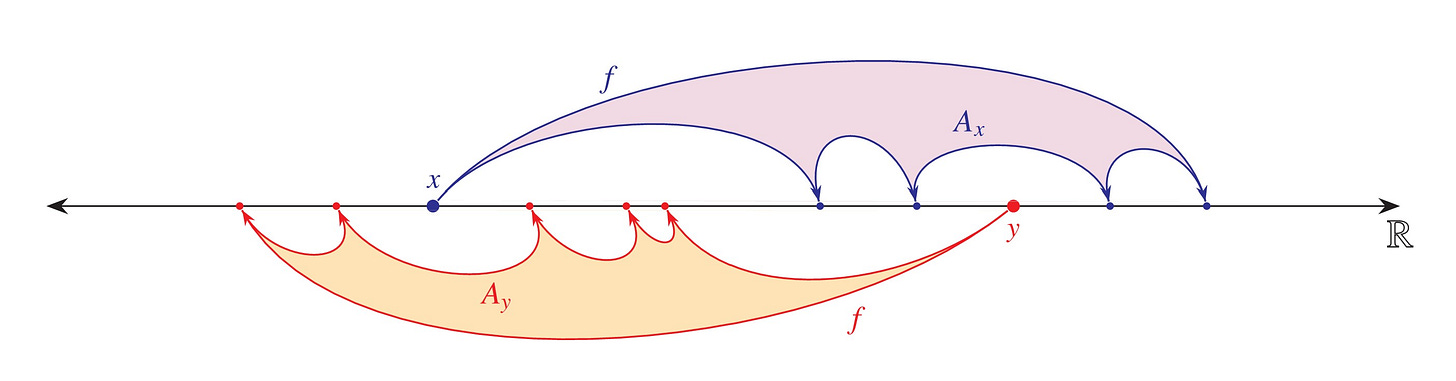
Chris Freiling, for example, proposed a thought experiment harnessing our intuitive ideas about probability and randomness to arrive at a conclusion about the continuum hypothesis. To begin, he supposes that we have associated every real number x with a certain countable set of real numbers A_x. In this situation, Freiling invites us to imagine throwing two darts at the real line. The first one lands at some real number x, and since the set A_x associated with that number is countable, almost surely the second dart will land at some place y that is not in A_x. The second point y is associated with its own set A_y.

By the symmetry of the situation, Freiling argues, we should similarly expect that x is not in A_y—it simply shouldn't matter which dart we think of as first. This line of thinking leads to Freiling's axiom of symmetry.

Axiom of Symmetry. For every association x ↦ A_x mapping reals to countable sets of reals, there are distinct real numbers x, y with y ∉ A_x and x ∉ A_y.

By throwing darts at the real line and appealing to primitive notions of probability, Freiling thus offers us a philosophical justification for his axiom.

The Axiom of Symmetry is Equivalent to the Negation of the Continuum Hypothesis

The principal mathematical observation to be made about the axiom of symmetry is that it is equivalent to the negation of the continuum hypothesis. Let me elaborate.

Enjoy this new installment from The Book of Infinity, a series of vignettes on infinity with all my favorite puzzles and paradoxes, serialized over the past year.

This installment features two thought experiments aimed at helping us resolve the problem of the continuum hypothesis.