We can predict the future
Is there a reliable strategy to predict the current and immediate future values of an arbitrary unknown function on the reals from the observed history of prior values?
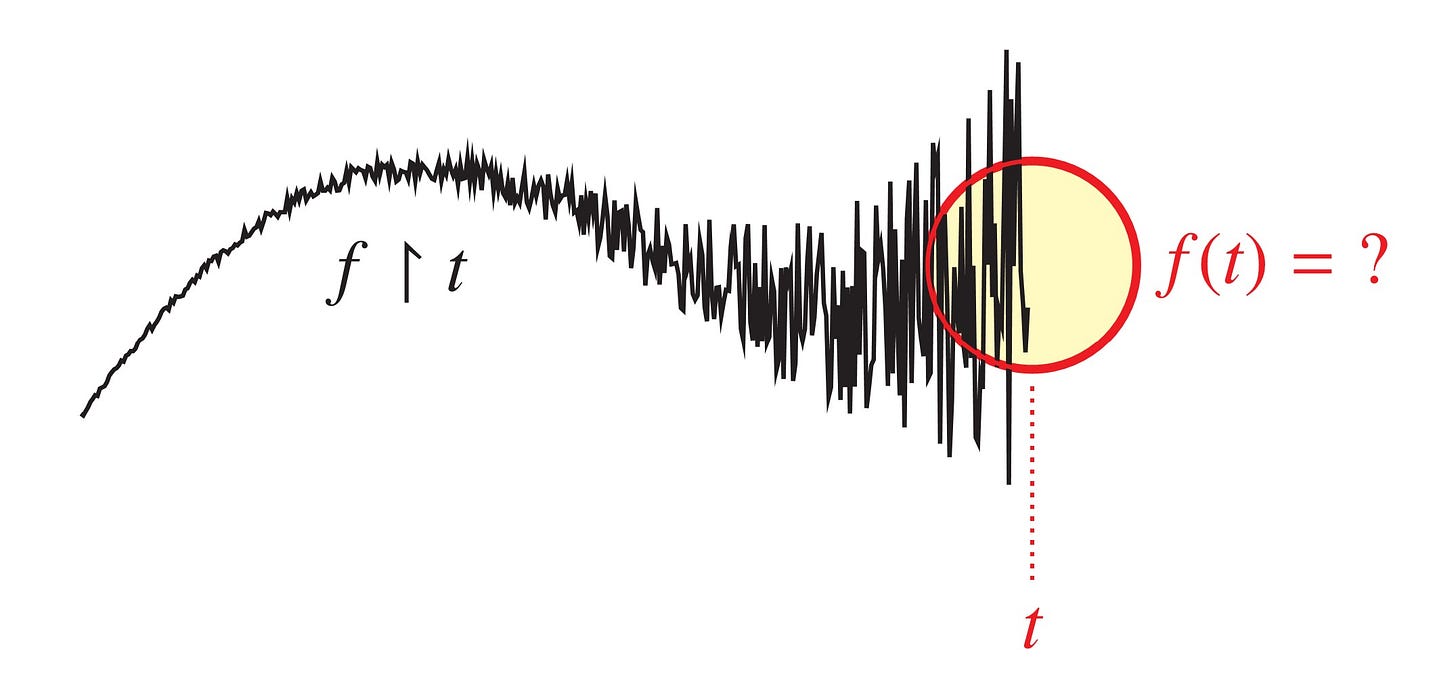
Suppose, like stock-market traders trying to guess today's opening price and price movements, we aim to predict the current and future values of an unknown function based on the observed history of previous values. The true function f:ℝ→ℝ will be revealed only gradually, and we seek to predict the current value f(t) at the current time t in light of the historical data, as well as to predict how the function will continue beyond t into the immediate future.
Predicting the present
Let us begin with the seemingly easier task of predicting the present. We want to predict the current value f(t) of the function f on the basis of its historical values before time t. Of course, if we knew somehow that the function were continuous, then we could easily predict the current value simply as the limit of the previous values.
The continuous case is thus a trivial kind of case for predicting the present—the limit value will be correct in every continuous instance.
The true function, however, might not be continuous—it could be very badly behaved, perhaps discontinuous at every point. And yet, nevertheless, we hope to predict the current value f(t) based on the history of the function until now. Let me emphasize that we are talking about predicting the values of the function exactly, not merely approximately. Close doesn't count.
In the general case, it may seem that no amount of information about the prior values f(x) for x < t would have any bearing on the current value—the true current value f(t) could be anything, to say nothing of the future values beyond t. Right? How could we possibly predict the correct value of f(t) with any reliable accuracy? Shouldn't it be completely hopeless for us to have a successful prediction strategy? We might hit upon a few lucky guesses, to be sure, but for any particular prediction procedure, wouldn't there be numerous possible functions that evade the predictions entirely?
Actually, no. The amazing mathematical fact, proved using the axiom of choice, is that there is a nearly perfect prediction strategy, one for which every function is predicted correctly at almost every point.
The proof casts us floundering in the deep philosophical waters of mathematical ontology. For although the proof establishes that indeed there is such a nearly perfect prediction strategy, unfortunately it does not reveal any useful details about the actual predictions that are to be made. This will be a pure-existence proof, showing that the strategy exists in the platonic realm of ideal forms, but without revealing sufficient information for us actually to implement it. You had best keep your day job.
To my way of thinking, nevertheless, even the pure mathematical existence of such a nearly perfect prediction method is astounding, and so let me tell you the story of this remarkable theorem, the nearly perfect prediction theorem, proved in 2008 by Christopher Hardin and Alan Taylor.
Enjoy this new installment from The Book of Infinity, a series of vignettes on infinity with all my favorite puzzles and paradoxes, serialized over the past year.
In this installment, we discuss and prove the nearly perfect prediction theorem, the remarkable result of Hardin and Taylor enabling us to predict the current and immediate future values of every function almost always, based on the observed historical data.