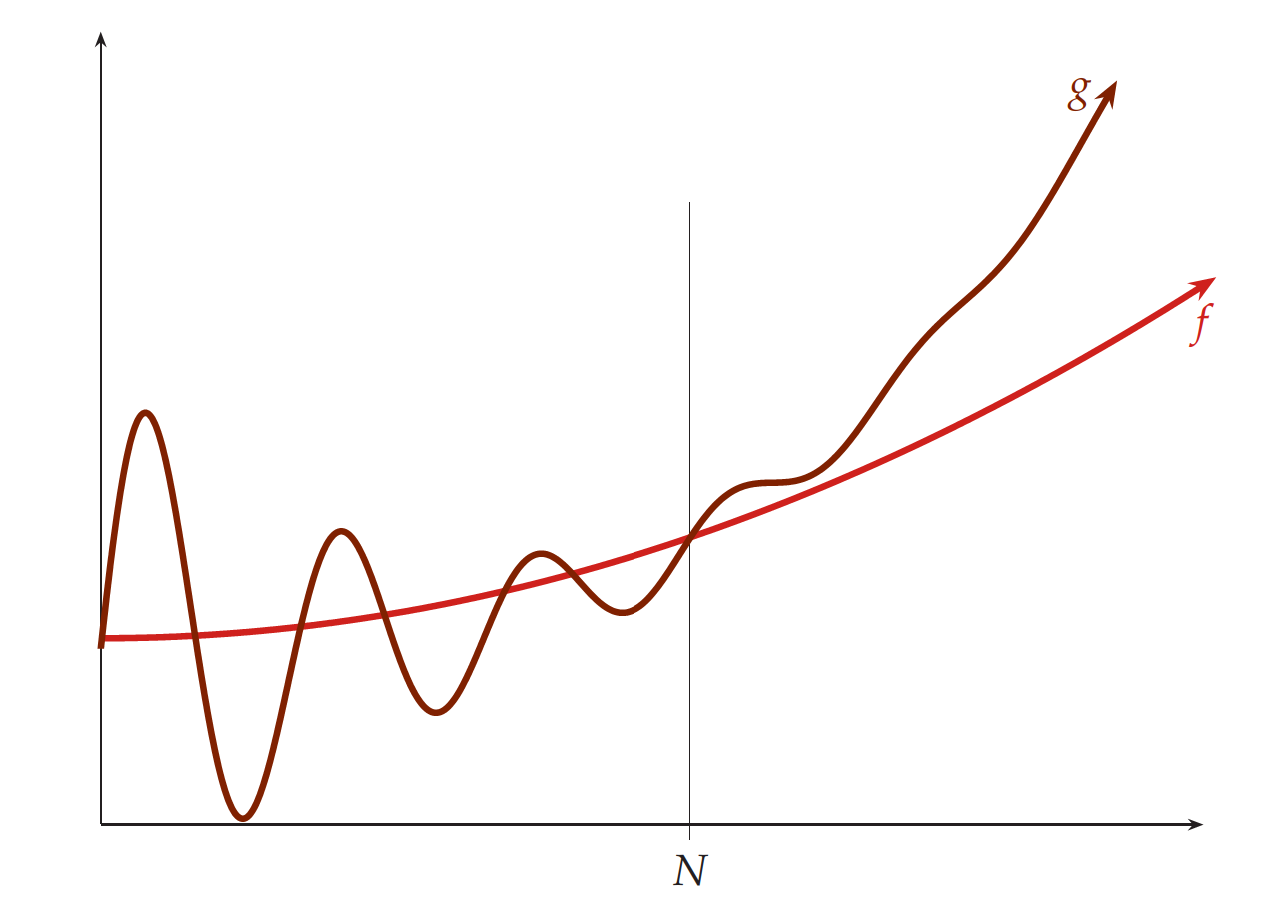
The eventual domination order

The mind-expanding property of the eventual domination order—every countable family of functions is strictly bounded. You cannot climb a simple ladder to the top.

The order of eventual domination f ≤* g holds of functions f, g : ℕ → ℕ when f(n) ≤ g(n) for all sufficiently large n, which is a precise compact way of saying that there is a natural number N such that f(n) ≤ g(n) for all n ≥ N. In other words, f ≤* g holds if eventually g(n) is at least as large as f(n). We similarly define the strict version f <* g, which means that f(n) < g(n) for all sufficiently large n.

This will be just a quick taste of the eventual domination order for Panorama of Logic. Some readers may be interested to read the longer gentle introduction to this topic that I provide in my essay The Orders of Infinity, written for The Book of Infinity.

I should like to prove Hausdorff’s theorem, identifying a remarkable feature of the eventual domination order. Namely, every countable sequence of functions is strictly bounded in the order of eventual domination. You cannot climb a simple ladder to the top.