The omnific integers are an integer part of the surreal numbers

Can we find a surreal-numbers analogue of the integers? An integer part of the surreal numbers, a discretely ordered subring, for which every surreal number is within 1.

This essay continues my ongoing series on the surreal numbers. This essay and all my other surreal numbers essays will appear in the tag surreal-numbers, with more content coming soon. Readers may wish to review basic notions in my introductory essay The Surreal Numbers, which offers a gentle introduction to this amazing and fantastical structure. For today, we continue the investigation by exploring the omnific integers!

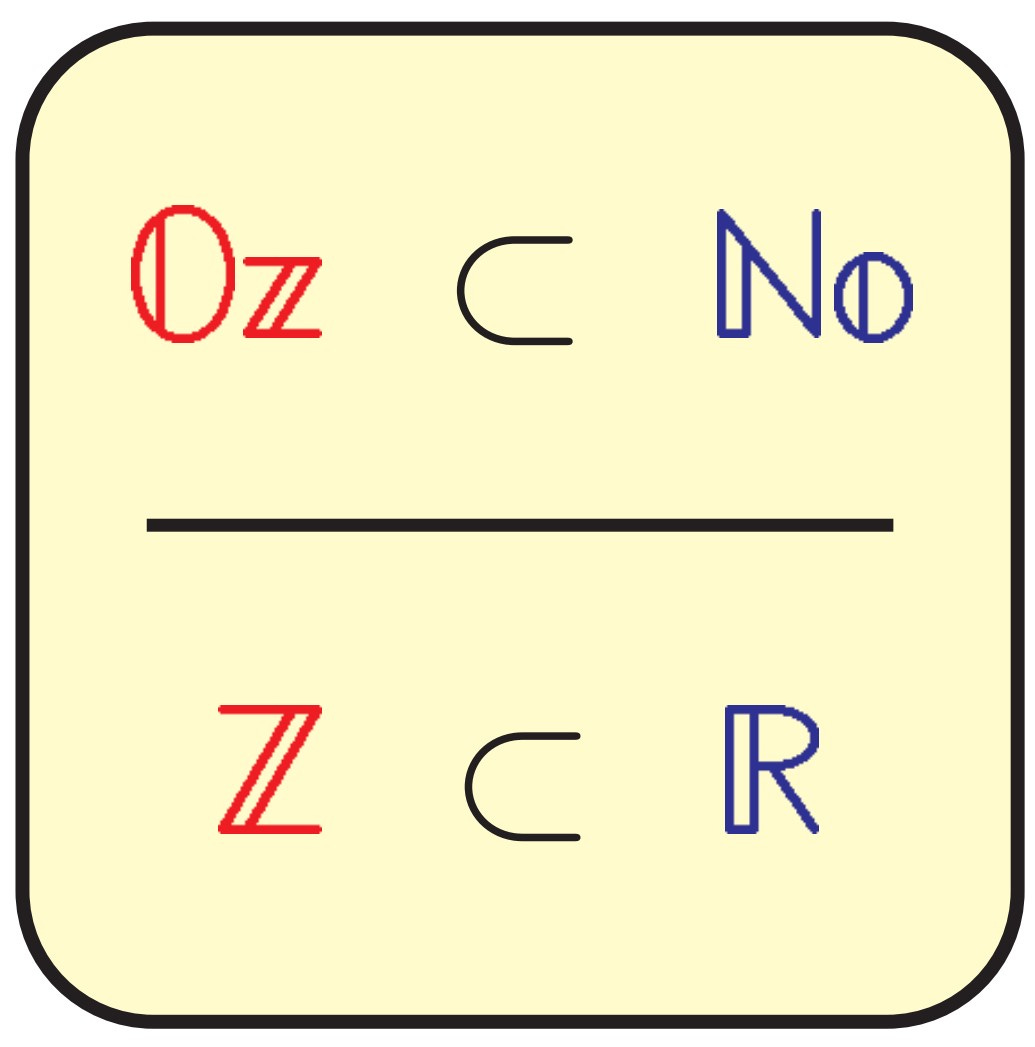
Consider how the familiar integers ℤ sit inside the field of real numbers ℝ.

Every integer has an immediate successor integer just above it and an immediate predecessor just below, and so the integers are discretely ordered. Indeed, this is a discrete order with a uniform unit step size—we get to the next or previous integer always by adding or subtracting one. What is more, we may freely add, subtract, and multiply integers while remaining within the integer realm, and so they constitute what is called a discretely ordered subring of the real field. Furthermore, the integers span the entire real line, in the sense that every unit interval [x, x + 1] in the real numbers contains an integer. The integers thus form an integer-part of the real numbers, the canonical instance of this concept.

If we consider the surreal number system as a colossal analogue of the real numbers, then it would seem very natural to inquire whether we can find a corresponding colossal analogue of the integers inside the surreal number system. Can we find an integer part of the surreal numbers? We would seek a discretely ordered subring of the surreal numbers that furthermore spans the surreal line in the same way that the integers sit inside the real numbers

Interlude

Yes, indeed we can. Let us discover together the class of Omnific integers, a vast yet discretely ordered subring Oz of the surreal numbers No, closed under addition, subtraction, and multiplication, and with every omnific integer having a successor and predecessor in the omnific integers, each at unit distance from the next. What is more, the omnific integers fully span the surreal line—every unit interval in the surreal numbers contains an omnific integer, and thus they form an integer part of the surreal field. In light of these features, the omnific integers can be viewed as a surreal-number analogue to the integers sitting in the real field.

Let us explore the nature and basic theory of the omnific integers Oz. Eventually, we shall also happen to uncover several subtle failures of this analogy.

I intend to provide several fundamentally different constructions and characterizations of the beautifully crystalline structure of the omnific integers Oz. One often gains insight into a mathematical idea, after all, by investigating it from diverse perspectives, thereby often revealing fundamentally different aspects of it, which can lead to a deeper understanding. So let us adopt this strategy with the omnific integers. We shall begin with a purely order-theoretic construction of the omnific integers, proceeding in a surreal-numbers-style transfinite gap-filling manner, thereby constructing the omnific integers as a universal saturated endless discrete linear order. By subsuming that construction into the surreal number gap-filling construction, we will arrive at a characterization of the omnific integers in terms of the nature of their surreal sign-sequence representations. Finally, we shall also provide the convenient Conway surreal numeral characterization of the omnific integers as those surreal numbers satisfying x = { x - 1 | x + 1 }. Ultimately, we shall prove that all these various accounts give rise to exactly the same class of numbers, the plenitudinous class Oz of the omnific integers.

Let us begin.