The surreal ω × ω chessboard is bigger—and stranger—than you think

What is the nature of the surreal ω × ω chessboard? How many squares are there? How many chess pieces shall we require to set up the board?

Welcome to this first essay in what will be a series on the surreal numbers, exploring all manner of curious topological aspects of the surreal field. Today we begin by looking into the nature of the surreal ω × ω chessboard. How many squares are there? How many pieces do we need to set up the board?

For a gentle introduction to the surreal numbers, readers may want to revisit my introductory essay The surreal numbers. You can also explore my surreal-number essays in the surreal-numbers tag, which will eventually include the upcoming essays in this series. Please enjoy!

Introduction

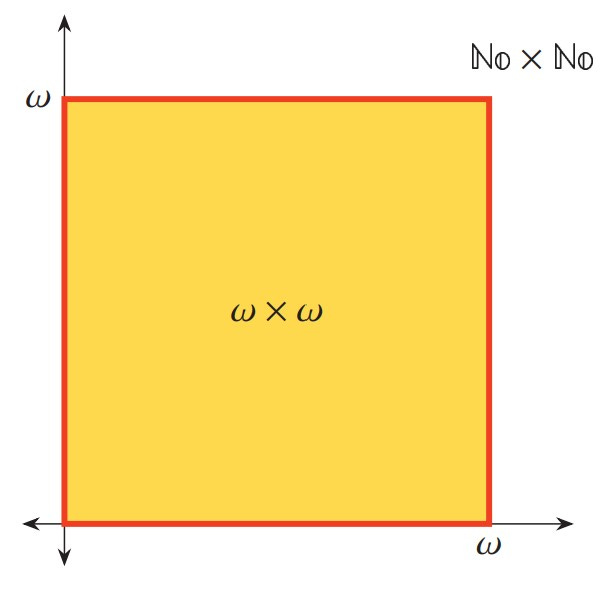
Consider the ω × ω square in the surreal plane, an abundant playing ground, a generous arena in the midst of the vast surreal field.

I propose to partition the edge segments [0,ω] of the square into surreal unit lengths and thereby aim to construct a chessboard on this playing field. Shall we have a game of surreal chess? Naturally I intend that we shall use full-size living chessmen—there will be dangerous armed characters and scheming courtesans roaming the chessboard amongst the furious mounted knights, their horses stomping and snorting hot steamy air. Let us play surreal chess on the surreal ω × ω chessboard!

We shall presently be calling upon our courts and armies in order to set up the chessboard. But before the game begins, we shall first have to answer a certain mathematical puzzle: how many chess pieces altogether do we require? How many pawns shall we call up, for example, if we aim to set them up as expected, respectively, on the second and penultimate ranks? For that matter, how many square tiles are there altogether on the surreal ω × ω chessboard?

Interlude

The answer is one that many people find surprising…

Please consider becoming a free or paid subscriber, with fresh content weekly on all aspects of infinity—mathematical, philosophical, and logical.

This is the first in a series of essays on the surreal numbers that will be released in coming weeks. In this particular essay, we explore the surprising nature of the surreal numbers as they are manifested in thinking about the surreal ω × ω chessboard.